При создании технологического процесса производства и проведении других проектных работ зачастую создаются чертежи. Они отражают особенности геометрии изделия, а также его размеры и многие другие моменты. Чертежи зубчатого колеса или другого типа выполняются по упрощенной схеме с применением различных условных обозначений. Это связано с тем, что сложная форма изделия создает существенные трудности при ее полной детализации на момент создания чертежей. Оформить рассматриваемый документ с учетом всех требований достаточно сложно, для этого требуются определенные навыки и знания. Сегодня большинство чертежей создается в электронном виде при применении особых программ. Стоит учитывать, что они лишь частично упрощают процесс. Часто проектируется червячная зубчатая передача, чертежи которой можно встретить на самых различных сайтах.
Механическое преимущество: крутящий момент против скорости вращения
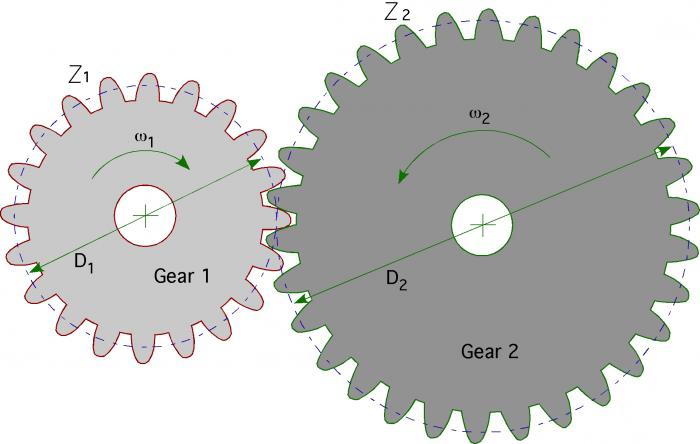
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.

Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной * Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.

Достоинства и недостатки


В сравнении с аналогами, имеющими другие конструкционные исполнения по действию, червячные зубчатые колеса более популярны. Узлы передачи выдают более высокий крутящий момент. При движении резьба червяка передвигается вдоль оси, что подталкивает и направляет зубы колеса в нужном направлении.
Основные достоинства зубчатых червячных колес следующие:
- компактные размеры, удобная сборка;
- высокий уровень передаточных чисел, 8-80, иногда до 100;
- бесшумная работа узла;
- плавный ход;
- система самоторможения.
Высокий уровень передаточных чисел позволяет увеличивать возможности снижения частоты вращения, возрастания крутящего момента. В узле колеса обеспечивают высокий уровень сцепления, что исключает шумы.
Пара червяк и червячное колесо обладает плавным ходом, способна вращаться в обеих направлениях. Позволяет производить наиболее плавное торможение при работе. При остановке движения передачи система самоторможения производит замедление скорости ведущего вала до полного стопа.
К недостаткам червячных зубчатых колес в редукторах относят следующие минусы:
- высокое трение вызывающее низкий КПД из-за повышенных параметров передаточного соотношения, энергетические потери;
- при избытке кинетической энергии и невозможности ее полной передачи возникает перегрев узла;
- заметный люфт выходных валов, возрастающий при интенсивной эксплуатации;
- относительно недолгий срок эксплуатации, в среднем до 10 тыс. часов.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Заказать расчет эвольвентного зацепления
Подсчитав все размеры элементов зацепления, приступаем к вычерчиванию зубчатого зацепления.
| Параметр зацепления | р | d1 | d2 | dв1 | dв2 | S1 | S2 | aw | dw1 | dw2 | da1 | da2 | df1 | df2 |
| Размер в масштабе, мм | 93,0 | 296,3 | 770,4 | 278,4 | 723,9 | 59,5 | 49,1 | 550,4 | 305,8 | 795,0 | 382,5 | 828,1 | 257,8 | 703,4 |
Пример расчета параметров зубчатого зацепления здесь.
Профили зубьев вычерчиваем в такой последовательности:
1. На чертеже под произвольным углом откладываем линию центров О1О2. Длина линии центров равна межосевому расстоянию О1О2=aw. 2. Из концов отрезка (линии центров) откладываем начальные окружности dw1 и dw2. Начальные окружности dw1 и dw2 касаются друг друга в полюсе P. 3. Откладываем и строим основные окружности dв1 и dв2.
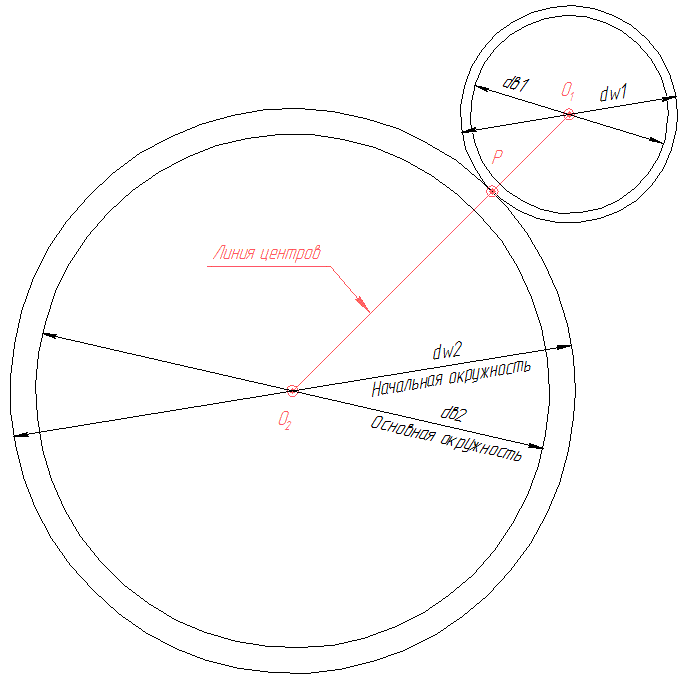

4. Построение эвольвенты колеса 2.
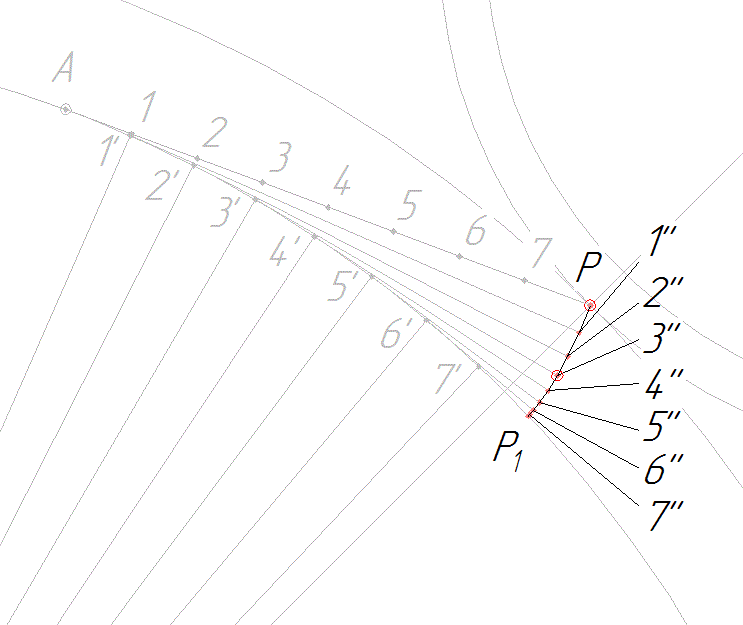
4.1. Из полюса P к основной окружности проводим касательную РА. Отрезок АР (см. рис.) делим на четыре равные части (АВ = ВС = СD = DP) и из точки В проводим дугу радиуса r = ВР до пересечения в точке Р1 с основной окружностью; тогда АР1 = АР.
4.2. После этого, отрезок АР снова делим на произвольное число равных частей длиной 15…20мм (число делений целесообразно взять четным, например 8). Дугу АР1 также делим на такое число равных частей (Р11’= 1′ 2′ = 2′ 3′ = …).
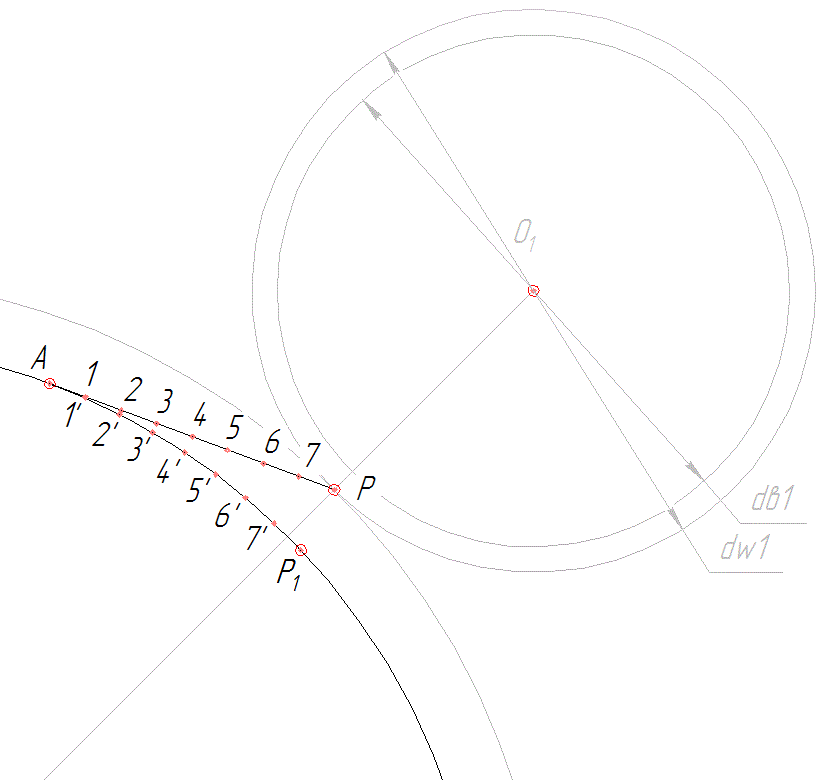

4.3. Точки 1′; 2′; 3’… соединяем с центром О2.
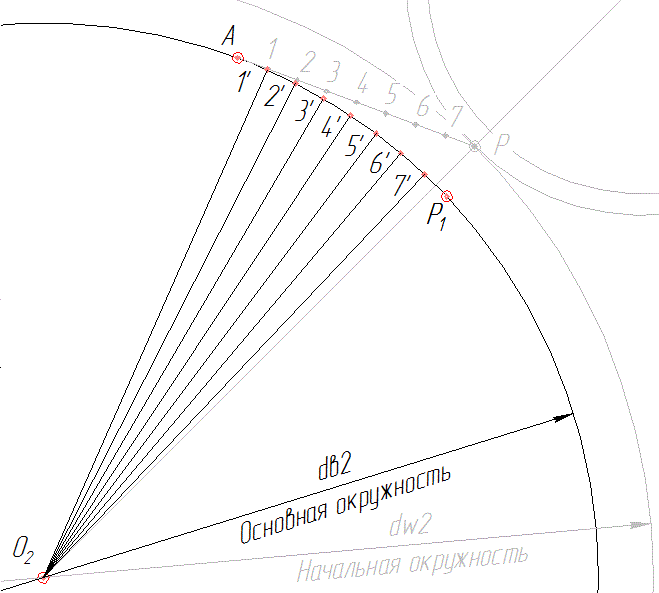

4.4. Через точки 1′; 2′; 3’… проводим перпендикуляры к соответствующим радиусам О21′; О22′; О23’…. На перпендикулярах (они касаются основной окружности) откладываем отрезки 1’1»; 2’2»; 3’3»…, соответственно равные отрезкам Р1; Р2; Р3….
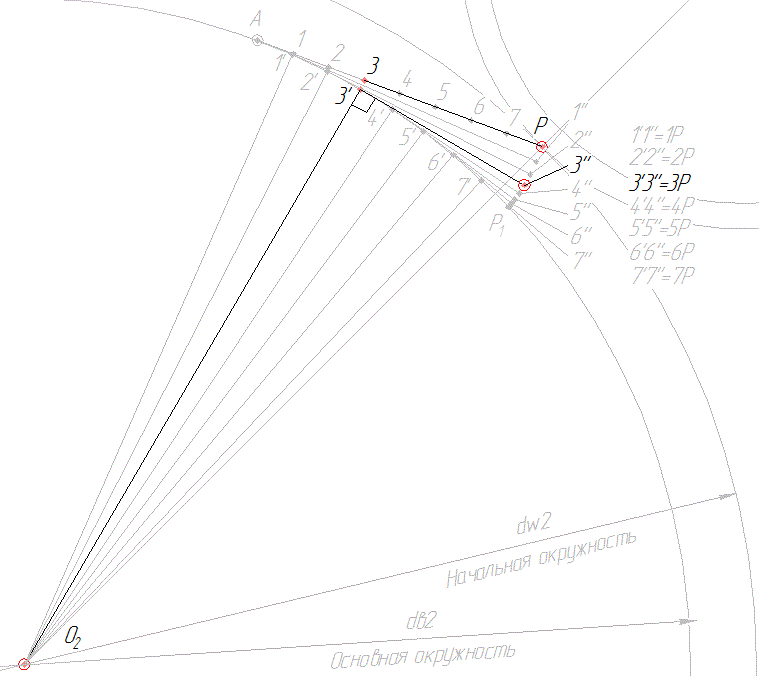

4.5. Соединяя точки Р1; 1»; 2»; 3»… плавной кривой, получаем часть эвольвенты второго колеса.

4.6. Для продолжения построения профиля зуба второго колеса откладываем и строим окружности выступов и впадин зубьев второго колеса. Следует отметить, что радиус окружности впадин может быть больше, равен и меньше радиуса rв основной окружности. Это зависит от числа Z зубьев колеса и от коэффициента смещения х. В нашем случае dв2 > df2
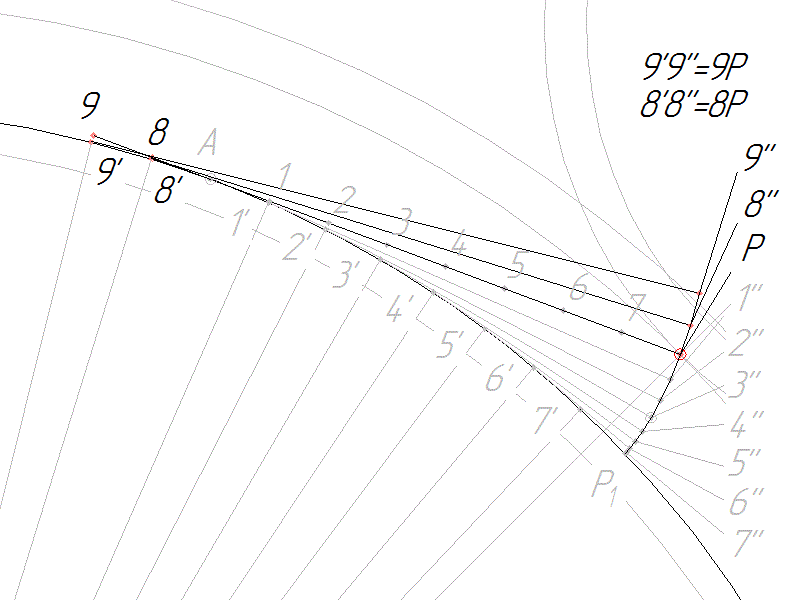
4.6. Для завершения построения эвольвенты второго колеса вводим дополнительные точки 8 и 9. Точки 8 и 9 откладываем против часовой стрелки от точки А. Пользуясь описанным выше методом, находим точки 8»и 9». Завершаем построение эвольвенты второго колеса.

4.7. Профиль ножки у основания зуба можно построить упрощенно. Если rf < rв, то от основания эвольвенты до окружности впадин проводят радиальный отрезок, а затем у основания зуба делают закругление радиуса 0,2m. Упрощенное построение профиля ножки зуба не отражают истинного его очертания, а является только чертежным приемом.
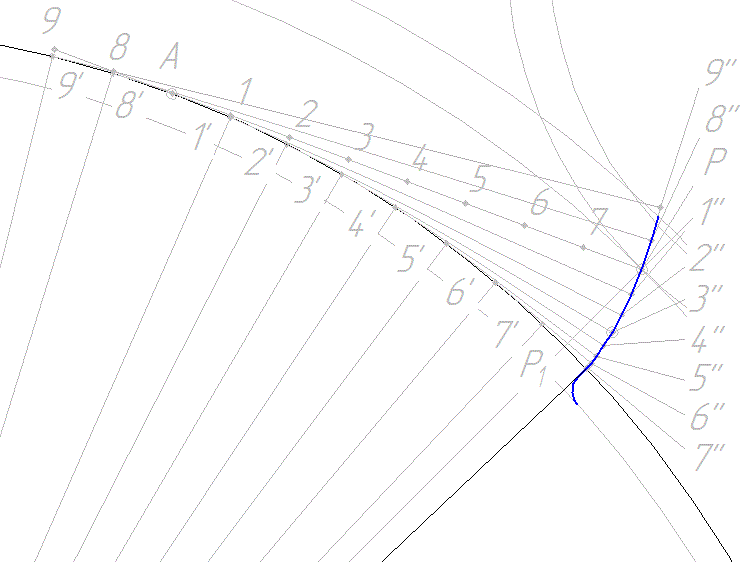

5. Строим делительную окружность колеса 2 и получаем точку D ее пересечения с эвольвентой.
От точки D откладываем на делительной окружности колеса 2 (пользуясь построением, показанным выше) дуги: влево DE, вправо DF, равные каждая длине шага р. От точки E, D, F влево откладываем (пользуясь тем же построением) дуги ER, DM, FH, равным каждая толщине S зуба по делительной окружности.
Делим дуги DM, FH, ER пополам в точках T, Y, Q. Соединяем эти точки с центром О2, получаем оси симметрии зубьев. После этого вырезаем из твердой бумаги шаблон половины зуба, которым пользуемся для построения остальных зубьев. Обязательным является построение трех зубьев – первого, профиль которого построен по точкам, и двух, находящихся справа и слева от первого.
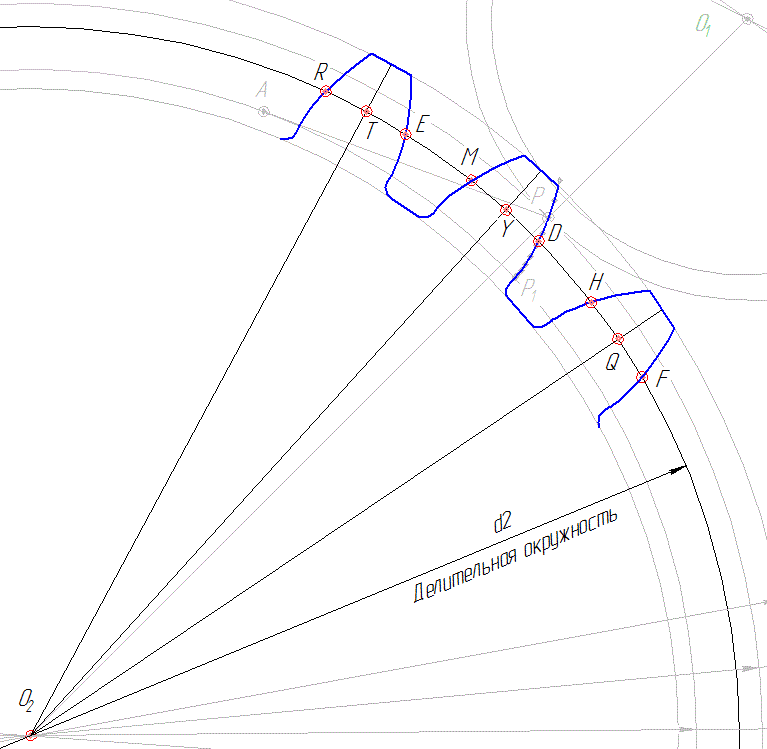

Аналогично строим три зуба для другого колеса.
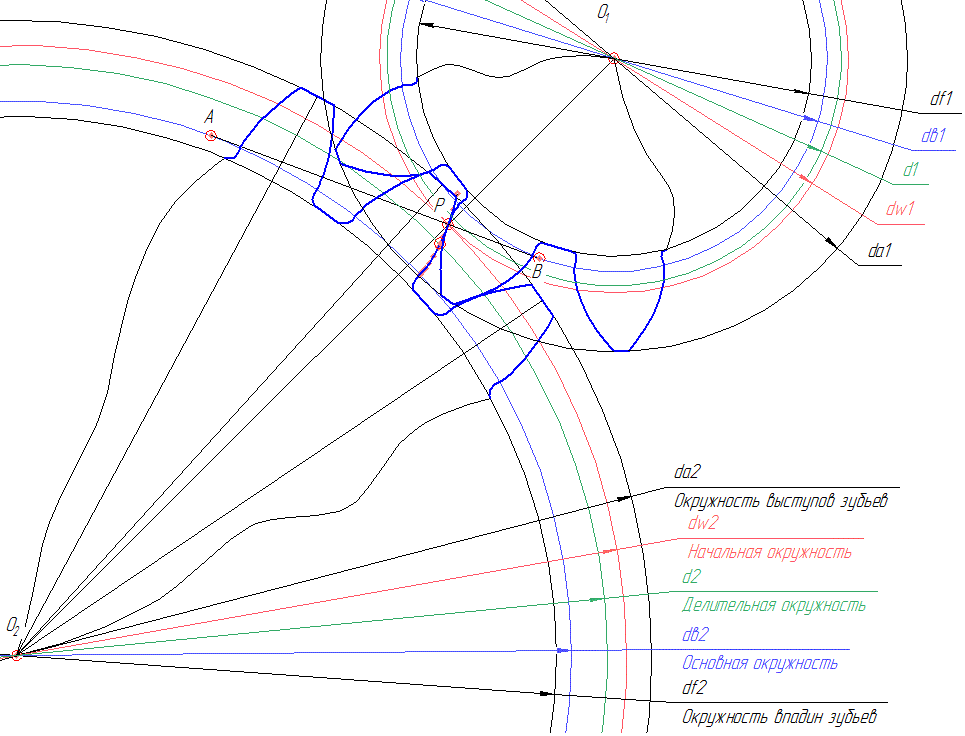

6. При вычерчивании профилей зубьев нужно помнить следующее: наличие зазора на активной части линии зацепления между профилями, пересекаемыми линий зацепления, свидетельствуют о неправильном выполнении чертежа.
Примеры ошибок:
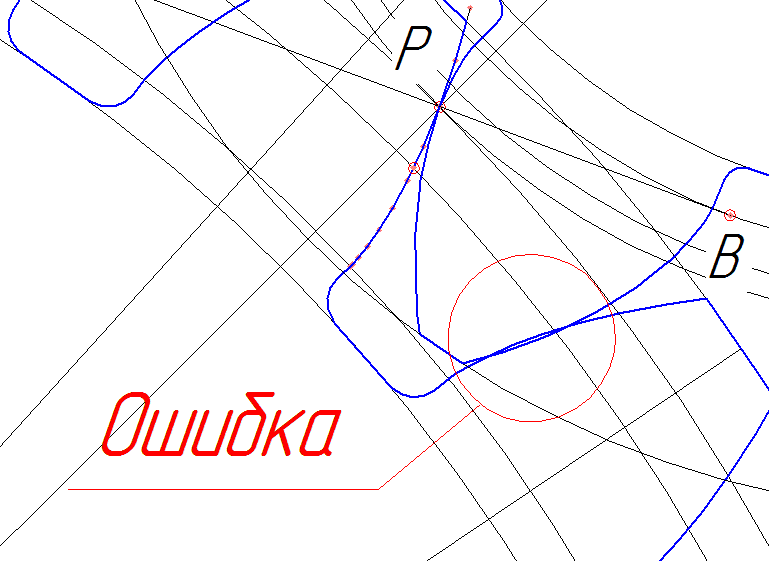

Заказать расчет эвольвентного зацепления
- < Назад
- Вперёд >
Комментарии
-1 Антоша 05.06.2017 04:13
Цитировать
Обновить список комментариев RSS лента комментариев этой записи
Добавить комментарий
JComments
Достижение определенного передаточного числа
Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).
Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая – 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.
Создаем 3D модель шестерни в программе Fusion 360.
Сейчас можно создать 3D модель для печати, на основании полученного эскиза. Для этого в программе Fusion 360 нажимаем на Sketch.
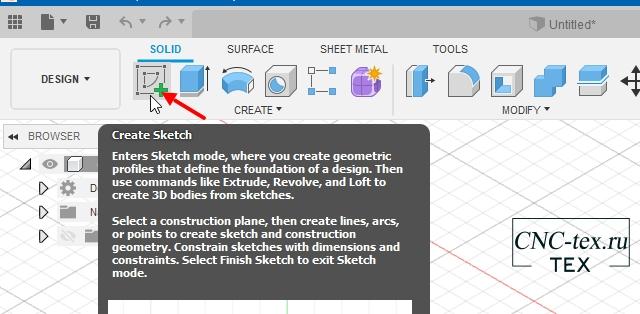

Выбираем плоскость, на которой будем создавать эскиз.
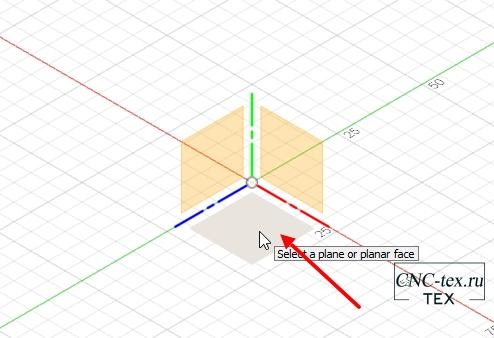

Затем в меню выбираем «Insert -> Insert SVG».
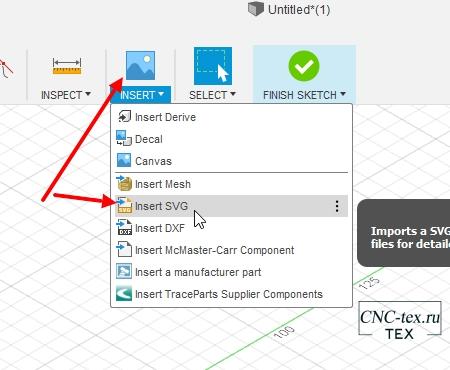

Нажимаем на кнопку загрузить с компьютера.
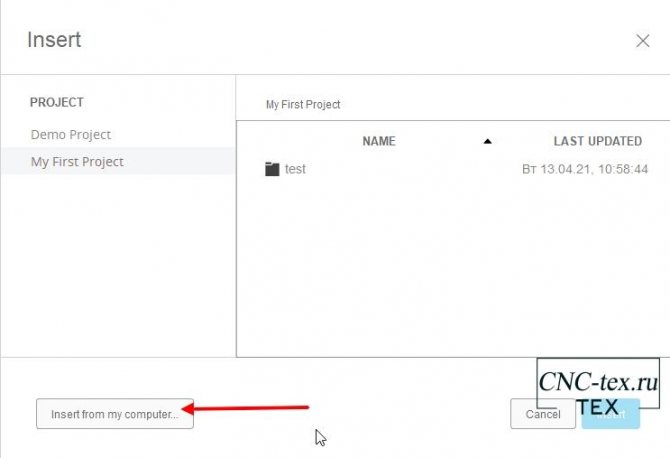

Выбираем файл, созданный в программе Inkscape.
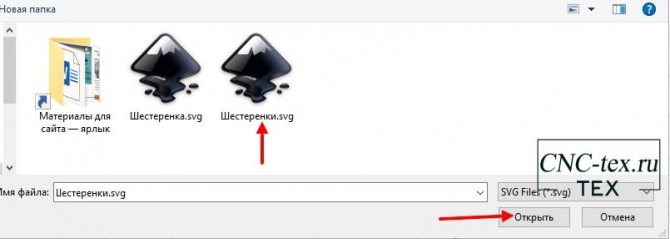

Внимание, важный момент!!!! При загрузке создастся эскиз, но гораздо меньше. Необходимо рассчитать коэффициент увеличения. Иначе вы получите вот такой результат, оранжевые детали сделаны без коэффициента увеличения.


Для расчета коэффициента, рисуем квадрат 100 на 100 мм. Загружаем в программу Fusion 360. Замеряем размер и 100 делим на полученное значение. У меня получился вот такой коэффициент: «3,795498538733063». Полностью значение можно не вводить. Но чем точнее значение, тем меньше будет отклонение в размере изделия. Я указал 3,795498.
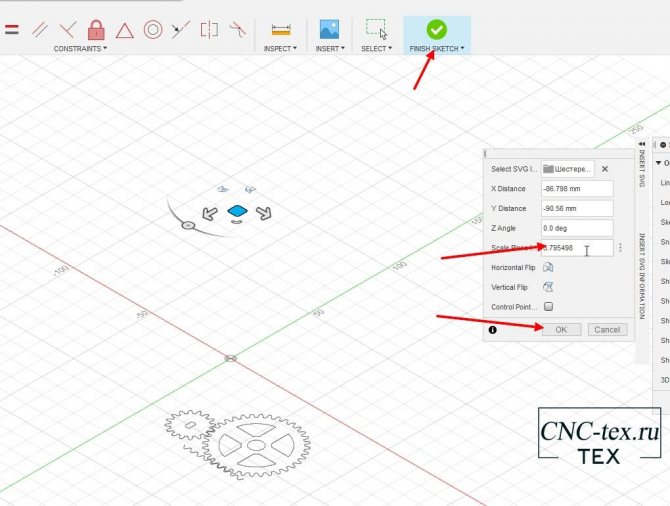

Затем выделяем деталь и нажимаем кнопку экстрадировать. Выдавливаем деталь на 5 мм.
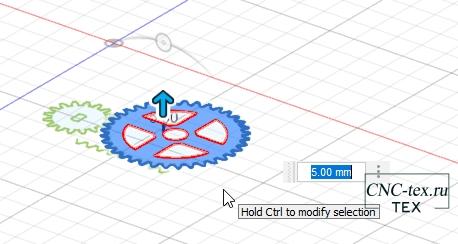

Вторую шестерёнку выдавливаем по аналогии.


Реечная передача в программе Fusion 360.
Если вы помните, мы не дорисовали реечную передачу в программе Inkscape. Поэтому нам нужно нарисовать её, для этого выбираем прямоугольник.
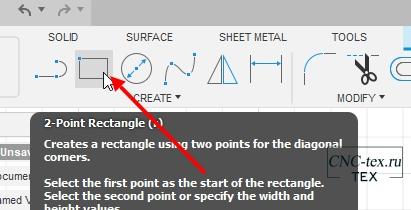

И рисуем по длине нашей рейки, нужной высоты.


Удаляем сторону прямоугольника, где у нас нарисованы зубцы рейки.
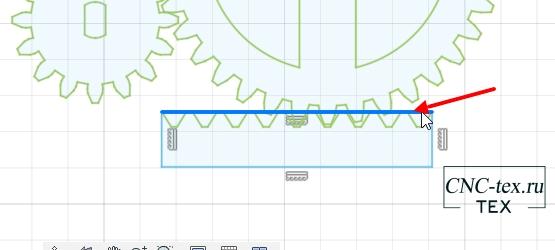

Затем экстрадируем полученную деталь.


В итоге получаем вот такой результат.
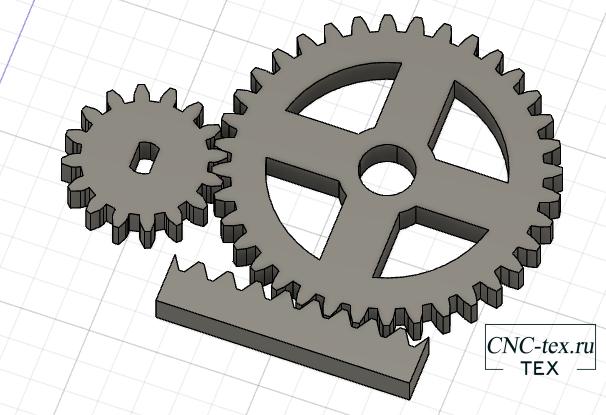

Как видим, все детали соединены точно так же, как и мы их нарисовали в программе Inkscape.
Эффективность передач
К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.
Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно
90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.
Если (из предыдущего примера):
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с,
Истинный Момент выходной = 1 Н∙м * 0,9= 0,9 Н∙м,
Истинная Скорость выходная = 150 об/с * 0,9 = 135 об/с.
Технология нарезки червячных зубчатых колес


Модель червячных шестерней создается в процессе проектирования изделия. Исходя из схемы можно определить метод нарезки:
- торцевой;
- подача фрезы снизу.
Торцевое нарезание червячных колес требует инструмента полностью аналогичного червяку. Устройство позволяет вести обработку с высокой точностью. Вставлять фрезу снизу сложно. Нужно чтобы ее положение относительно вала точно соответствовало червяку.
На венце нарезка зубьев выполняется фрезами, имеющими наружный диаметр одинаковый с червяком. Инструмент повторяет форму ведущего элемента, но линия не непрерывная, вместо нее ряды резцов.
По конфигурации режущая пластина должна точно повторять резьбовую нитку, при этом она должна быть шире на величину зазора. В итоге форма червячного колеса высокоточно аналогична форме резьбы. Ее впадины полностью совпадают с выступами нитей.
Выставление фрезы выполняется в осевой плоскости червяка с прикосновением к поверхности изделия. Вращение зубчатого венца происходит вокруг собственного вала или вертикальной оправки. Это обеспечивает тангенциальную подачу внешней поверхности по оси резца.
Нарезка червячных зубчатых колес выполняется в синхронном передвижении детали и инструмента, оборачивающихся вокруг собственных осей. Скорость вращения устанавливается передаточным числом. Каждый оборот венца подвигает его ближе к крутящейся фрезе.
Режущий инструмент подают как сверху, так и снизу. На практике предпочтение отдают радиальной нарезке. Метод самый удобный и высокоточный.
Ремонтная нарезка выполняется при необходимости сделать одну деталь для замены в редукторе. В мастерских не всегда можно найти фрезу необходимого диаметра. При применении большего инструмента прилегание станет хуже, уменьшится пятно контакта. Нарезка фрезой меньшего диаметра увеличит нагрузку на верхнюю часть нити. В обоих случаях отремонтированное таким образом колесо будет иметь высокий износ, трение. КПД при этом также упадет. Поэтому выполнять нарезку необходимо резцами с точно совпадающим диаметром.
Направление вращения шестерен
Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.
Конструкция и параметры зубчатого колеса
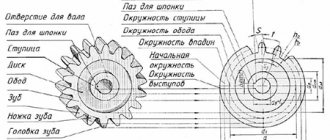
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
Читать также: Свариваемость сталей между собой таблица
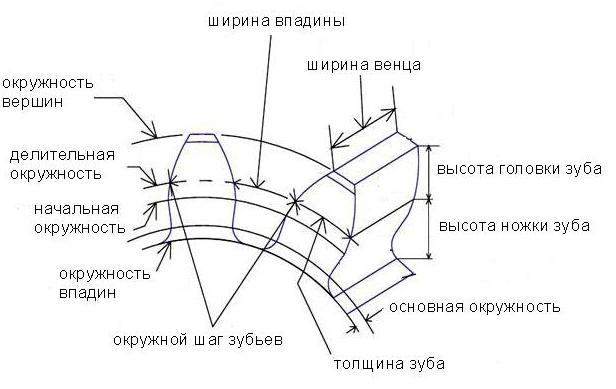

Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Основные данные
Червячное зубчатое колесо является главной деталью передачи. Представляет собой диск конической, цилиндрической формы с расположенными на верхней его плоскости зубьями. При помощи последних во время вращения выполняется зацепление зубчатого колеса с червяком, что позволяет переносить вращательный момент от вала с шестерней на другой шпиндель.
Зубья одного элемента толкают аналоги на другом, которые приводят в действие свою ось. Вал, на котором находится червяк, начинает совершать вращение, передавать движение к другим элементам конструкции. Прибор или установка начинают функционировать и выполнять свои задачи.
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 – 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
Создание чертежа зубчатого колеса
Кроме создания моделей, данная библиотека позволяет строить плоские чертежи, при этом они создаются аннотативными и если в будущем из них можно создать трехмерную модель.
Для создания такого чертежа, создадим файл чертежа и откроем библиотеку Приложения – Механика – Валы и механические передачи 2D – построение модели. Выберем Элементы механических передач – Шестерни и зубчатые рейки – Цилиндрическая шестерня с внешними зубьями, либо другую из списка. Открылось окно с данными цилиндрической шестерни. Как видим, большая часть полей не активна и без данных. В разделе Тип передачи можно изменить тип зацепления. Для введения данных для построения шестерни нажмем кнопку Запуск расчета.
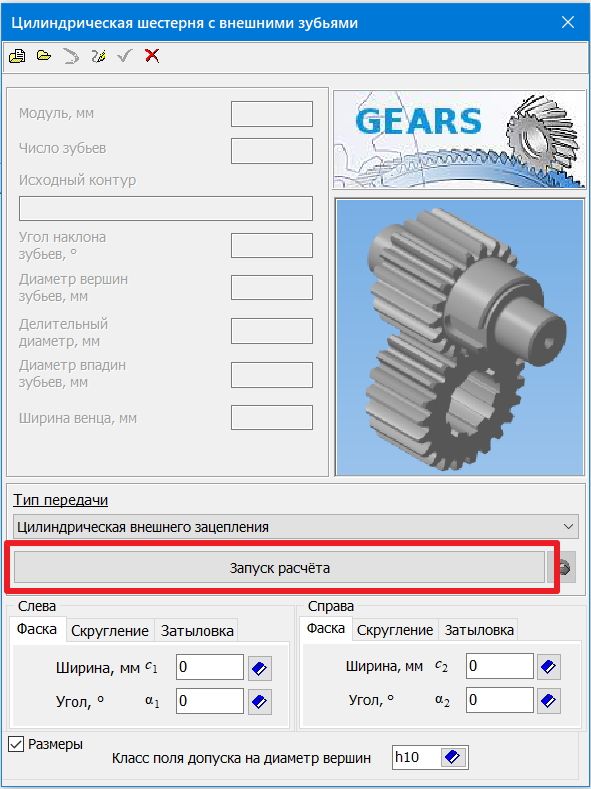

Окно данных для построения шестерни
Как и ранее выберем в появляющихся окнах Геометрический расчет и подходящий вариант расчета. Далее так-же как и при трехмерном моделировании заполним таблицу данных геометрического расчета нашей будущей шестерни. Для продолжения расчета обязательно нужно заполнять обе колонки Ведущего колеса и Ведомого колеса, иначе 2 страница будет недоступна. Если для вам работы работы нужно создать только одно колесо, то такие данные второго колеса, как число зубьев и ширина зубчатого венца можно ввести произвольные.
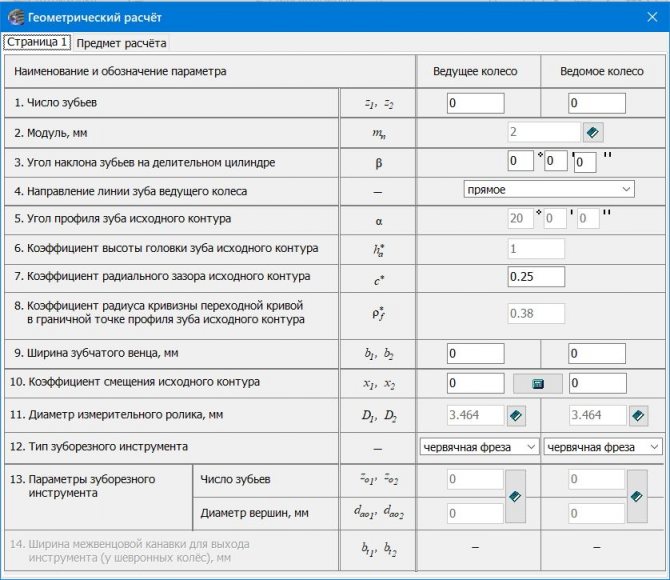

Окно геометрических параметров шестерни
Далее повторяем все действия как и в предыдущем разделе о построении трехмерной модели шестерни. После ввода всех данных появится окно с уже введенными параметрами. В нижней части окна можно задать параметры фаски, скругления и затыловки.
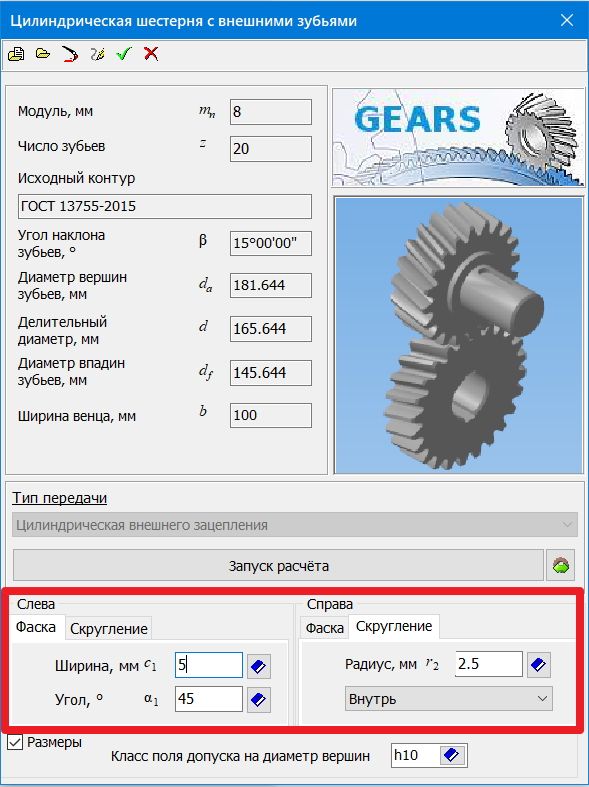

Окно данных для построения шестерни с введенными параметрами шестерни
Для завершения нажмем OK в верхней части окна.
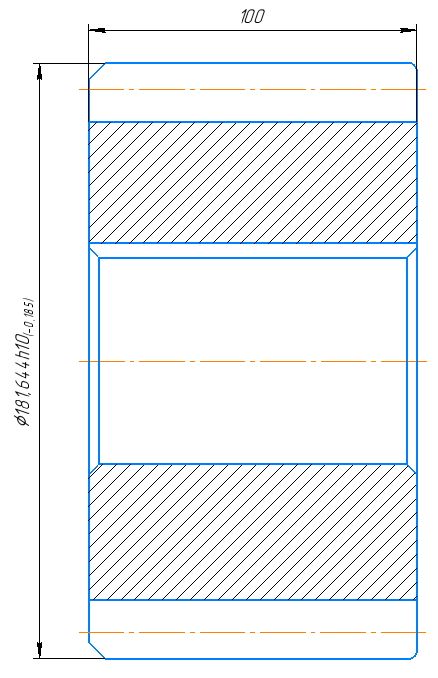

Получившийся чертеж шестерни
Для редактирования чертежа, в дереве построения выберем строку с надписью Макро:36 (цифры могут быть другими) и нажмем Редактировать макроэлемент. После чего в появившемся окне Валы и механические передачи 2D выбрать из списка требующуюся шестерню и кликнуть на нее два раза левойк нопкой мыши.

Редактирование макроэлемента
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.
Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
ГОСТ 2.402-68 ЕСКД. Условные изображения зубчатых колес, реек, червяков и звездочек цепных передач
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ
ПРАВИЛА ВЫПОЛНЕНИЯ ЧЕРТЕЖЕЙ РАЗЛИЧНЫХ ИЗДЕЛИЙ
УСЛОВНЫЕ ИЗОБРАЖЕНИЯ ЗУБЧАТЫХ КОЛЕС, РЕЕК, ЧЕРВЯКОВ И ЗВЕЗДОЧЕК ЦЕПНЫХ ПЕРЕДАЧ
ГОСТ 2.402-68 (СТ СЭВ 286-76)
МОСКВА — 1998
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
| Единая система конструкторской документации УСЛОВНЫЕ ИЗОБРАЖЕНИЯ ЗУБЧАТЫХ КОЛЕС, PEEK, ЧЕРВЯКОВ И ЗВЕЗДОЧЕК ЦЕПНЫХ ПЕРЕДАЧ Unified system for design documentation. Conventional representation of gears, racks, worms and chain wheels | ГОСТ 2.402-68 (CT СЭВ 286-76) Взамен ГОСТ 3460-59 |
Утвержден Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР в декабре 1967 г. Срок введения установлен
с 01.01.71
1. Настоящий стандарт устанавливает условные изображения, применяемые при выполнении чертежей зубчатых колес, реек, червяков и звездочек цепных передач, а также при выполнении сборочных чертежей, содержащих указанные детали.
Стандарт соответствует CT СЭВ 286-76.
2. Условные изображения зубчатых колес, реек, червяков, звездочек цепных передач должны быть выполнены по правилам, изложенным в пп. 3 — 12, и соответствовать чертежам, указанным в табл. 1 и 2.
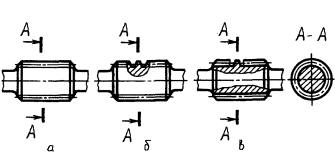
3. Зубья зубчатых колес, звездочек цепных передач и витки червяков вычерчивают в осевых разрезах и сечениях, зубья реек — в поперечных.
В остальных случаях зубья и витки не вычерчивают и изображаемые детали ограничивают поверхностями выступов (табл. 1, черт. 1 — 9).
Если необходимо показать профиль зуба или витка, вычерчивают зуб или виток на выносном элементе; допускается показывать их на ограниченном участке изображения детали (табл. 1,черт. 1б
, 6).
4. Окружности и образующие поверхностей выступов зубьев и витков (цилиндров, конусов и т.п.) показывают сплошными основными линиями, в том числе и в зоне зацепления (табл. 1, черт. 1 — 9; табл. 2, черт. 1 — 4, 9, 11, 12).
5. На чертежах зубчатых колес, реек, червяков, звездочек цепных передач показывают делительные окружности, делительные линии, образующие делительных поверхностей (цилиндров, конусов и т.п.) и окружности больших оснований делительных конусов (табл. 1, черт. 1 — 6, 8, 9).
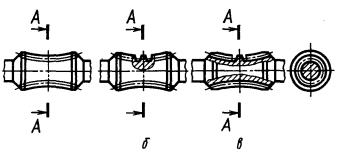
6. На сборочных чертежах зубчатых и червячных передач показывают начальные окружности, начальные линии, образующие начальных поверхностей и окружности больших оснований начальных конусов (табл. 2, черт. 1 — 11).
7. На чертежах глобоидных червяков и сопрягаемых с ними колес, а также на сборочных чертежах глобоидных червячных передач показывают расчетные окружности и образующие расчетных поверхностей (табл. 1, черт. 7; табл. 2, черт. 12).
8. Делительные, начальные, расчетные окружности и линии, образующие делительных, начальных и расчетных поверхностей, окружности больших оснований делительных и начальных конусов показывают штрихпунктирными тонкими линиями.
9. Окружности и образующие поверхностей впадин зубьев и витков в разрезах и сечениях показывают на всем протяжении сплошными основными линиями.
На видах цилиндрических зубчатых колес, червяков, реек и звездочек цепных передач допускается показывать окружности и образующие поверхностей впадин зубьев или витков, при этом их наносят сплошными тонкими линиями (табл. 1, черт. 1б
, 8; табл. 2, черт. 1
а
).
10. Если секущая плоскость проходит через ось зубчатого колеса или звездочки, то на разрезах и сечениях зубчатых колес и звездочек, а также на поперечных разрезах и сечениях реек и червяков зубья и витки условно совмещают с плоскостью чертежа и показывают нерассеченными независимо от угла наклона зуба и угла подъема витка (табл. 1, черт. 1 — 9).
11. Если секущая плоскость проходит перпендикулярно к оси зубчатого колеса или звездочки, вдоль червяка или вдоль рейки, то зубчатые колеса, звездочки, червяки и рейки, как правило, показывают нерассеченными.
При необходимости показать их рассеченными применяют местный разрез и проводят штриховку до линии поверхности впадин (табл. 2, черт. 11б
).
12. Если секущая плоскость проходит через оси обоих зубчатых колес, находящихся в зацеплении, то на разрезе в зоне зацепления зуб одного из колес (предпочтительно ведущего) показывают расположенным перед зубом сопрягаемого колеса (табл. 2 , черт. 1 а
, 2 , 4
а
, 5 — 7 ).
Если секущая плоскость проходит через ось червячного колеса или червяка, то виток червяка показывают расположенным перед зубом колеса (табл. 2, черт. 11, 12).
Если секущая плоскость проходит через ось зубчатого колеса реечного зацепления, то зуб колеса показывают перед зубом рейки (табл. 2, черт. 3).
В перечисленных случаях невидимые контуры допускается не наносить, если это не затрудняет чтение чертежа.
13. Если необходимо показать направление зубьев зубчатого колеса, рейки или витков червяка, то на изображение поверхности зубьев или витков наносят (как правило, вблизи оси) три сплошные тонкие линии с соответствующим наклоном.
На изображении зубчатого или реечного зацепления направление зубьев указывают на одном из элементов зацепления (табл. 2, черт. 1б
,
в
,
г
, 4
б
; 9).
14. При изображении зацепления коническими зубчатыми колесами с пересечением осей под углом, отличным от прямого, коническое колесо, ось которого наклонена к плоскости проекции, параллельной оси парного колеса, изображают окружностью большего основания начального конуса, совмещенного с плоскостью чертежа; то же колесо, проецируемое на плоскость, перпендикулярную к оси парного колеса, изображают треугольником, вершина и основание которого получаются проецированием вершины и диаметра большого основания начального конуса (табл. 2, черт. 5, 6).
15. При изображении винтового зацепления с пересечением осей под углом, отличным от прямого, колесо, ось которого наклонена к плоскости проекций, изображают начальной окружностью, совмещенной с плоскостью чертежа (табл. 2, черт. 10).
16. При изображении цепных передач цепь показывают штрихпунктирной тонкой линией, соединяющей делительные окружности звездочек (табл. 2, черт. 13).
Таблица 1
| Наименование | Условное изображение |
| 1. Колесо зубчатое цилиндрическое | Черт. 1 |
| 2. Колесо зубчатое цилиндрическое с внутренними зубьями | Черт. 2 |
| 3. Колесо зубчатое коническое | Черт. 3 |
| 4. Колесо зубчатое плоское | Черт. 4 |
| 5. Колесо зубчатое червячное | Черт. 5 |
| 6. Червяк цилиндрический |
Черт. 6 |
| 7. Червяк глобоидный |
Черт. 7 |
| 8. Рейка зубчатая | Черт. 8 |
| 9. Звездочка цепной передачи | Черт. 9 |
Таблица 2
| Наименование | Условное изображение |
| 1. Зацепление внешнее цилиндрическими зубчатыми колесами | Черт. 1 |
| 2. Зацепление внутреннее цилиндрическими зубчатыми колесами | Черт. 2 |
| 3. Зацепление реечное | Черт. 3 |
| 4. Зацепление внешнее коническими зубчатыми колесами с пересечением осей под прямым углом | Черт. 4 |
| 5. Зацепление внешнее коническими зубчатыми колесами с пересечением осей под углом, отличным от прямого | Черт. 5 |
| 6. Зацепление плоскоконическое | Черт. 6 |
| 7. Зацепление паллоидное | Черт. 7 |
| 8.Зацепление гипоидное | Черт. 8 |
| 9. Зацепление винтовое цилиндрическими зубчатыми колесами с пересечением осей под прямым углом | Черт. 9 |
| 10. Зацепление винтовое цилиндрическими зубчатыми колесами с пересечением осей под углом, отличным от прямого | Черт. 10 |
| 11. Зацепление с цилиндрическим червяком | Черт. 11 |
| 12. Зацепление с глобоидным червяком | Черт. 12 |
| 13. Цепная передача | Черт. 13 |
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Цилиндрические прямозубые колеса (КПД
Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.


Цилиндрические косозубые колеса (КПД
Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.


Червячные передачи (КПД
Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).
Для выполнения расчетов, чертежей и эскизов зубчатых колёс и других деталей зубчатых передач надо знать основные элементы и параметры зубчатых зацеплений и условности, принятые для изображения зубчатого венца.
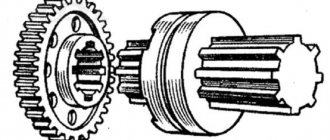
Рис. 17. Шестерни с элементами фиксации на валу
Основным элементом зубчатого колеса является зуб.
Начальная поверхность делит зуб по его высоте на две неравные части – головку и ножку. Часть зуба, расположенная над делительной поверхностью, называется головкой зуба, а расположенная ниже делительной поверхности – ножкой зуба. Зубья с ободом составляют венец зубчатого колеса, который через диск или спицы соединён со ступицей, имеющей отверстие для вала, зачастую с элементами фиксации колеса на валу, например, при помощи шпоночного (рис. 17,
а
) или шлицевого (рис. 17,
б)
соединений.
Читать также: Максимальная длина сливного шланга посудомоечной машины
Конструкция
Колеса с зубьями конструкционно могут представлять собой следующие формы:
- диск;
- обод со спицами, крепящимися к расположенной в центре него втулке;
- цельный цилиндр.
По внешнему периметру в различном количестве, в зависимости от диаметра червячного колеса, сделаны выемки. Конфигурация наружной поверхности напоминает форму зубов, поэтому и получила название зубчатое колесо. Параметры червячных передач указаны нормами по ГОСТ 2144-76


Внутри шестерни, строго по центру находится отверстие, предназначенное для крепления колеса к рабочему валу. Для создания надежного сцепления между ними предусмотрена специальная выемка для крепежной шпильки. Она же позволяет при износе зубьев быстро сменить вышедшую из строя шестерню на новую.
Чертежи конструкции зубчатое колесо бывают нередко довольно сложными. В них могут быть следующие элементы:
- отверстие для вала;
- ступица;
- шпоночный паз;
- диск;
- обод;
- ножка зуба;
- зуб;
- головка зуба;
- образующая делительного цилиндра;
- окружность впадин;
- делительная окружность;
- окружность зубьев.
Варианты конструкций могут быть самые разнообразные. Производители изготавливают шестерни для червячных передач различных типов. Но во всех модификациях выделяют три основных компонента. Первый, зубчатый венец, являющийся главным элементом, на который приходится вся нагрузка при работе. Второй компонент – расположенная в центре диска ступица, со сквозным отверстием для крепления вала. Форма последнего может быть следующих видов:
- цилиндрическая;
- квадратная;
- многоугольная.
Третьим общим компонентом для зубчатых колес является диск. С целью экономии металла при производстве изделий у него толщина меньше, чем у обода, ступицы. Нередко в диске сделаны с той же целью отверстия, различного диаметра, форм.