Механическое преимущество: крутящий момент против скорости вращения
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.

Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной* Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.
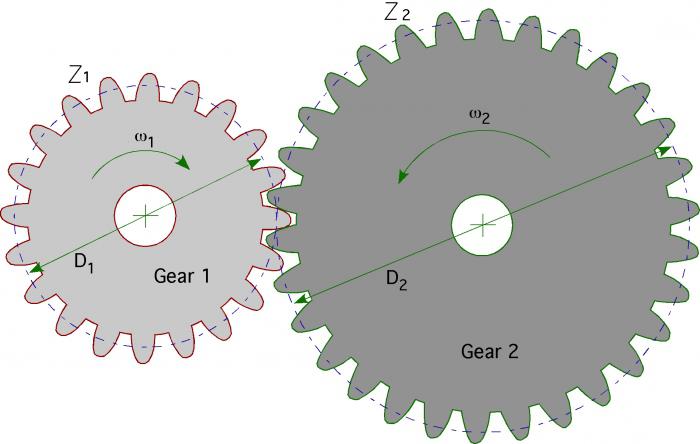

Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
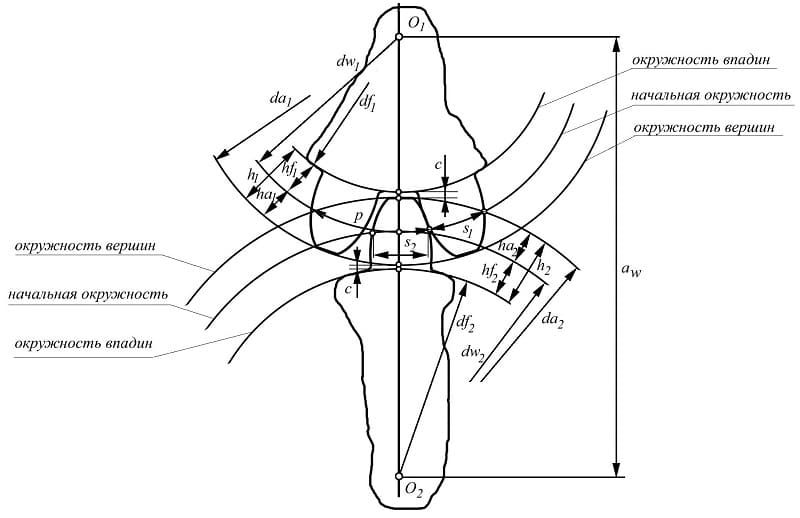

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Пример:
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Примерные значения КПД различных передач
| Вид передачи | Закрытая | Открытая |
| Цилиндрическая зубчатая передача | 0.96…0.98 | 0.93…0.95 |
| Коническая зубчатая передача | 0.95…0.97 | 0.92…0.94 |
| Червячная передача — самотормозящая z1=1 — несамотормозящая z1=1 z1=2 z1=4 | 0.45 0.68…0.72 0.73…0.78 0.78…0.84 | 0.40 0.52…0.62 0.62…0.72 |
| Цепная передача | 0.95…0.97 | 0.90…0.93 |
| Плоскоременная передача | —— | 0.93…0.95 |
| Клиноременная передача | —— | 0.94…0.96 |
| Фрикционная передача | 0.90…0.96 | 0.70…0.80 |
| Одна пара подшипников качения | 0.990…0.995 | |
| Муфта | 0.98…0.99 |
Примечание:
рекомендуется брать среднее значение в указанном интервале.
Таблица 2
Рекомендуемые передаточные числа различных передач
| Вид передачи | Среднее передаточное число | Максимально возможное передаточное число |
| Открытая цилиндрическая зубчатая передача | 3…7 | |
| Закрытая цилиндрическая зубчатая передача | 3…6 | |
| Закрытая коническая зубчатая передача | 2…3 | |
| Открытая червячная передача | 10…60 | |
| Закрытая червячная передача | 10…40 | |
| Открытая цепная передача | 2…6 | |
| Открытая плоскоременная передача | 2…5 | |
| Открытая клиноременная передача | 2…5 |
Примечание:
рекомендуется брать среднее значение в указанном интервале.
Таблица 3
Стандартные значения передаточных чисел u
| 1 ряд | 1,00 | 1,25 | 1,6 | 2,00 | 2,50 | 3,15 | 4,0 | 5,0 | 6,3 | 8,0 | 10,0 | 12,5 | 16,0 | 20,0 | 31,5 |
| 2 ряд | 1,12 | 1,40 | 1,8 | 2,24 | 2,8 | 3,55 | 4,5 | 5,6 | 7,1 | 9,0 | 11,2 | 14,0 | 18,0 | 22,4 | 35,5 |
Примечание:
Лучше округлять до ближайшего значения из любого ряда, при равных условиях следует предпочитать первый ряд.
Таблица 4
Параметры асинхронных электродвигателей
| Тип электродвигателя | Pэд, кВт | nэд, мин-1 | Тпик/Тном | Масса, кг |
Синхронная частота вращения 3000
| 4А71А2У3 | 1,1 | 2,0 | 12,0 |
| 4А80А2У3 | 1,5 | 2,0 | 14,0 |
| 4А80В2У3 | 2,2 | 2,0 | 16,0 |
| 4А90L2У3 | 3,0 | 2,0 | 25,0 |
| 4A100S2У3 | 4,0 | 2,0 | 34,0 |
| 4A100L2У3 | 5,5 | 2,0 | 60,0 |
| 4A112M2У3 | 7,5 | 2,0 | 71,0 |
| 4A132M2У3 | 11,0 | 2,0 | |
| 4A160S2У3 | 15,0 | 2,0 | |
| 4A160M2У3 | 18,5 | 1,9 | |
| 4A180S2У3 | 22,0 | 1,9 |
Синхронная частота вращения 1500
| 4A80A4У3 | 1,1 | 2,0 | 14,0 |
| 4A80B4У3 | 1,5 | 2,0 | 17,2 |
| 4A90L4У3 | 2,2 | 2,0 | 25,0 |
| 4A100S4У3 | 3,0 | 2,0 | 26,0 |
| 4A100L4У3 | 4,0 | 2,0 | 34,0 |
| 4A112M4У3 | 5,5 | 2,0 | 62,0 |
| 4A132SУ3 | 7,5 | 2,0 | 73,0 |
| 4A132M4У3 | 11,0 | 2,0 | |
| 4A1604SУ3 | 15,0 | 2,0 | |
| 4A160M4У3 | 18,5 | 1,9 | |
| 4A180S4У3 | 22,0 | 1,9 |
Таблица 4
(продолжение)
Синхронная частота вращения 1000
| 4A80B6У3 | 1,1 | 1,9 | 15,6 |
| 4A90L6У3 | 1,5 | 1,9 | 24,0 |
| 4A100L6У3 | 2,2 | 1,9 | 33,0 |
| 4A112MA6У3 | 3,0 | 1,9 | 54,0 |
| 4A112MB6У3 | 4,0 | 1,9 | 66,0 |
| 4A132S6У3 | 5,5 | 1,9 | 72,0 |
| 4A132M6У3 | 7,5 | 1,8 | |
| 4A160S6У3 | 11,0 | 1,8 | |
| 4A160M6У3 | 15,0 | 1,8 | |
| 4A180M6У3 | 18,5 | 1,8 | |
| 4A200M6У3 | 22,0 | 1,8 |
Синхронная частота вращения 750
| 4A90LB8У3 | 1,10 | 1,8 | 26,3 |
| 4A100L8У3 | 1,50 | 1,8 | 31,0 |
| 4A112MA8У3 | 2,20 | 1,8 | 53,0 |
| 4A112MB8У3 | 3,00 | 1,8 | 65,0 |
| 4A132S8У3 | 4,00 | 1,8 | 85,0 |
| 4A132M80У3 | 5,50 | 1,8 | 95,0 |
| 4A160S8У3 | 7,50 | 1,7 | |
| 4A160M8У3 | 11,0 | 1,7 | |
| 4A180M8У3 | 15,0 | 1,7 | |
| 4A200M8У3 | 18,5 | 1,7 | |
| 4A200L8У3 | 22,0 | 1,7 |
ЛИТЕРАТУРА
1. Детали машин: Учебник для машиностроительных специальностей вузов/ М.Н. Иванов, В.А. Финогенов – 8-е изд.,испр.– М.: Высш. шк., 2003.– 408с.: ил.
2. Детали машин/ К.И. Заблонский.– К.: Вища шк. Головное изд-во, 1985.– 518с.
3. Дунаев П.Р., Леликов О.П. Конструирование деталей и узлов машин. М.: Высшая школа, 2001. – 447с.
4. Дьяконов В. Mathcad 2001: Специальный справочник. – СПб.: Питер, 2002.– 832с.: ил.
5. Кирьянов Д.В. Самоучитель Mathcad 11.- СПб.: БХВ-Петербург, 2003.- 560с.: ил.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1. Кинематический расчет привода 4
1.1. Выбор электродвигателя 4
Разбивка передаточного числа 5
Определение параметров вращения валов привода 5
2. ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА ПРИВОДА, ВКЛЮЧАЮЩЕГО ДВЕ СТУПЕНИ 6
2.1. Выбор электродвигателя 7
2.2. Разбивка передаточного числа 7
2.3. Оптимизация разбивки передаточного числа 8
Определение параметров вращения валов привода 8
3. ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА ПРИВОДА, ВКЛЮЧАЮЩЕГО ТРИ СТУПЕНИ 10
3.1. Выбор электродвигателя 10
Разбивка передаточного числа 11
Определение параметров вращения валов привода 12
ПРИЛОЖЕНИЕ 14
ЛИТЕРАТУРА 17
| Вид передачи | Закрытая | Открытая |
| Цилиндрическая зубчатая передача | 0.96…0.98 | 0.93…0.95 |
| Коническая зубчатая передача | 0.95…0.97 | 0.92…0.94 |
| Червячная передача — самотормозящая z1=1 — несамотормозящая z1=1 z1=2 z1=4 | 0.45 0.68…0.72 0.73…0.78 0.78…0.84 | 0.40 0.52…0.62 0.62…0.72 |
| Цепная передача | 0.95…0.97 | 0.90…0.93 |
| Плоскоременная передача | —— | 0.93…0.95 |
| Клиноременная передача | —— | 0.94…0.96 |
| Фрикционная передача | 0.90…0.96 | 0.70…0.80 |
| Одна пара подшипников качения | 0.990…0.995 | |
| Муфта | 0.98…0.99 |
Примечание:
рекомендуется брать среднее значение в указанном интервале.


Таблица 2
Рекомендуемые передаточные числа различных передач
| Вид передачи | Среднее передаточное число | Максимально возможное передаточное число |
| Открытая цилиндрическая зубчатая передача | 3…7 | |
| Закрытая цилиндрическая зубчатая передача | 3…6 | |
| Закрытая коническая зубчатая передача | 2…3 | |
| Открытая червячная передача | 10…60 | |
| Закрытая червячная передача | 10…40 | |
| Открытая цепная передача | 2…6 | |
| Открытая плоскоременная передача | 2…5 | |
| Открытая клиноременная передача | 2…5 |
Примечание:
рекомендуется брать среднее значение в указанном интервале.
Таблица 3
Стандартные значения передаточных чисел u
| 1 ряд | 1,00 | 1,25 | 1,6 | 2,00 | 2,50 | 3,15 | 4,0 | 5,0 | 6,3 | 8,0 | 10,0 | 12,5 | 16,0 | 20,0 | 31,5 |
| 2 ряд | 1,12 | 1,40 | 1,8 | 2,24 | 2,8 | 3,55 | 4,5 | 5,6 | 7,1 | 9,0 | 11,2 | 14,0 | 18,0 | 22,4 | 35,5 |
Примечание:
Лучше округлять до ближайшего значения из любого ряда, при равных условиях следует предпочитать первый ряд.
Таблица 4
Параметры асинхронных электродвигателей
| Тип электродвигателя | Pэд, кВт | nэд, мин-1 | Тпик/Тном | Масса, кг |
Синхронная частота вращения 3000
| 4А71А2У3 | 1,1 | 2,0 | 12,0 |
| 4А80А2У3 | 1,5 | 2,0 | 14,0 |
| 4А80В2У3 | 2,2 | 2,0 | 16,0 |
| 4А90L2У3 | 3,0 | 2,0 | 25,0 |
| 4A100S2У3 | 4,0 | 2,0 | 34,0 |
| 4A100L2У3 | 5,5 | 2,0 | 60,0 |
| 4A112M2У3 | 7,5 | 2,0 | 71,0 |
| 4A132M2У3 | 11,0 | 2,0 | |
| 4A160S2У3 | 15,0 | 2,0 | |
| 4A160M2У3 | 18,5 | 1,9 | |
| 4A180S2У3 | 22,0 | 1,9 |
Синхронная частота вращения 1500
| 4A80A4У3 | 1,1 | 2,0 | 14,0 |
| 4A80B4У3 | 1,5 | 2,0 | 17,2 |
| 4A90L4У3 | 2,2 | 2,0 | 25,0 |
| 4A100S4У3 | 3,0 | 2,0 | 26,0 |
| 4A100L4У3 | 4,0 | 2,0 | 34,0 |
| 4A112M4У3 | 5,5 | 2,0 | 62,0 |
| 4A132SУ3 | 7,5 | 2,0 | 73,0 |
| 4A132M4У3 | 11,0 | 2,0 | |
| 4A1604SУ3 | 15,0 | 2,0 | |
| 4A160M4У3 | 18,5 | 1,9 | |
| 4A180S4У3 | 22,0 | 1,9 |
Таблица 4
(продолжение)
Синхронная частота вращения 1000
| 4A80B6У3 | 1,1 | 1,9 | 15,6 |
| 4A90L6У3 | 1,5 | 1,9 | 24,0 |
| 4A100L6У3 | 2,2 | 1,9 | 33,0 |
| 4A112MA6У3 | 3,0 | 1,9 | 54,0 |
| 4A112MB6У3 | 4,0 | 1,9 | 66,0 |
| 4A132S6У3 | 5,5 | 1,9 | 72,0 |
| 4A132M6У3 | 7,5 | 1,8 | |
| 4A160S6У3 | 11,0 | 1,8 | |
| 4A160M6У3 | 15,0 | 1,8 | |
| 4A180M6У3 | 18,5 | 1,8 | |
| 4A200M6У3 | 22,0 | 1,8 |
Синхронная частота вращения 750
| 4A90LB8У3 | 1,10 | 1,8 | 26,3 |
| 4A100L8У3 | 1,50 | 1,8 | 31,0 |
| 4A112MA8У3 | 2,20 | 1,8 | 53,0 |
| 4A112MB8У3 | 3,00 | 1,8 | 65,0 |
| 4A132S8У3 | 4,00 | 1,8 | 85,0 |
| 4A132M80У3 | 5,50 | 1,8 | 95,0 |
| 4A160S8У3 | 7,50 | 1,7 | |
| 4A160M8У3 | 11,0 | 1,7 | |
| 4A180M8У3 | 15,0 | 1,7 | |
| 4A200M8У3 | 18,5 | 1,7 | |
| 4A200L8У3 | 22,0 | 1,7 |
ЛИТЕРАТУРА
1. Детали машин: Учебник для машиностроительных специальностей вузов/ М.Н. Иванов, В.А. Финогенов – 8-е изд.,испр.– М.: Высш. шк., 2003.– 408с.: ил.
2. Детали машин/ К.И. Заблонский.– К.: Вища шк. Головное изд-во, 1985.– 518с.
3. Дунаев П.Р., Леликов О.П. Конструирование деталей и узлов машин. М.: Высшая школа, 2001. – 447с.
4. Дьяконов В. Mathcad 2001: Специальный справочник. – СПб.: Питер, 2002.– 832с.: ил.
5. Кирьянов Д.В. Самоучитель Mathcad 11.- СПб.: БХВ-Петербург, 2003.- 560с.: ил.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1. Кинематический расчет привода 4
1.1. Выбор электродвигателя 4
Разбивка передаточного числа 5
Определение параметров вращения валов привода 5
2. ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА ПРИВОДА, ВКЛЮЧАЮЩЕГО ДВЕ СТУПЕНИ 6
2.1. Выбор электродвигателя 7
2.2. Разбивка передаточного числа 7
2.3. Оптимизация разбивки передаточного числа 8
Определение параметров вращения валов привода 8
3. ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА ПРИВОДА, ВКЛЮЧАЮЩЕГО ТРИ СТУПЕНИ 10
3.1. Выбор электродвигателя 10
Разбивка передаточного числа 11
Определение параметров вращения валов привода 12
ПРИЛОЖЕНИЕ 14
ЛИТЕРАТУРА 17
Достижение определенного передаточного числа
Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).
Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая — 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.
Направление вращения шестерен
Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
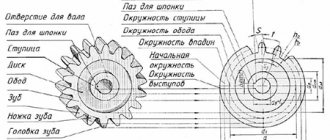
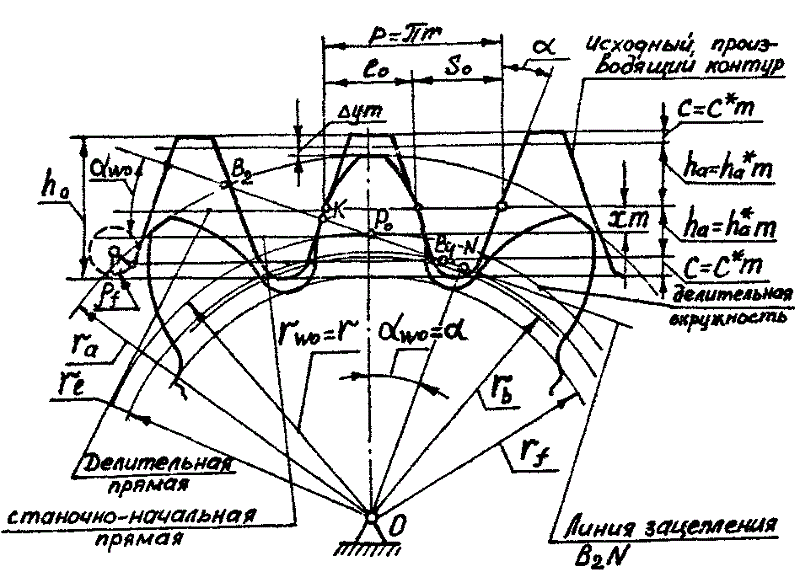
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
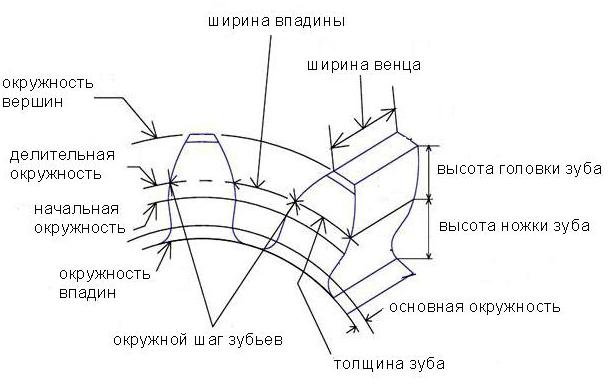

Делительная окружность показана на нем пунктиром. По ней принято определять окружной шаг зубьев p (шаг зацепления), т. е. часть ее длины, приходящуюся на один зуб, и модуль шестерни m – часть диаметра делительной окружности d, приходящуюся на один зуб. Чтобы его вычислить, просто используйте формулу ниже:
m = d/z= p/3,14, мм.
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Окружная скорость зубчатых колес
По значению скорости назначаем 8-ю степень точности изготовлениязубчатых колес
Проверка контактной выносливости поверхностей зубьев
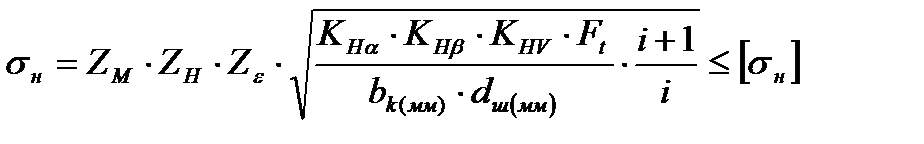
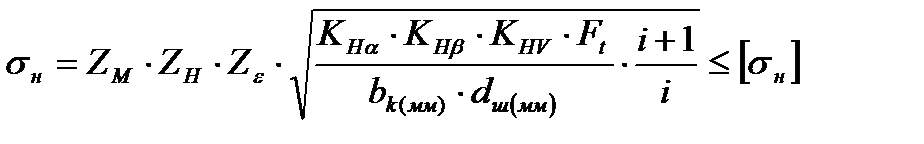
Допускаемые контактные напряжения
ZМ
– коэффициент, учитывающий механические свойства материалов сопряженных зубьев,
ZМ
= 275
ZH
– коэффициент, учитывающий форму зубьев
Угол профиля зуба αt
=20°, β=0
Ze
– коэффициент, учитывающий суммарную длину контактных линий
для прямозубых передач;
где εα
– торцевой коэффициент перекрытия
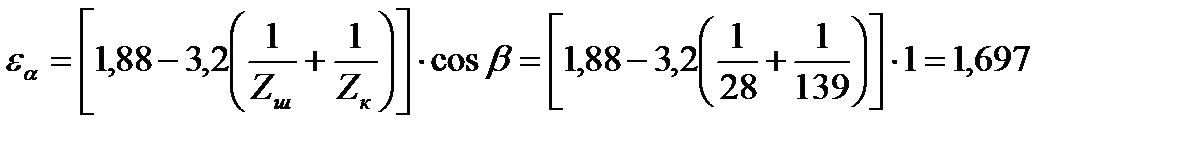
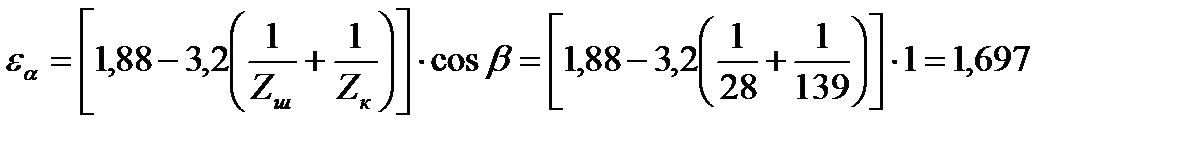
KHa
– коэффициент неравномерности распределения нагрузки между зубьями.
KHa
=1 для прямозубых передач
KHb
– коэффициент неравномерности распределения нагрузки по длине зуба.
KHb
= 1,02
KHV
– коэффициент динамической нагрузки.
KHV
=1,05
Ft
– окружная сила
Рассчитываем контактные напряжения
Проверка контактной прочности поверхности зубьев при кратковременных перегрузках
Проверка выносливости зубьев при изгибе
Ft
– окружная сила,
KFa
– коэффициент неравномерности распределения нагрузки между зубьями,
KFa
= 1,321
KFβ
– коэффициент неравномерности распределения нагрузки по длине,
KFβ
= 1,05
KFV
– коэффициент динамической нагрузки,
KFV
= 1,25
– коэффициент, учитывающий форму зуба
Таблица 10 – Зависимость коэффициента от эквивалентного числа зубьев
| ZV | ||||||||||||||
| yF | 4,25 | 4,11 | 4,01 | 3,92 | 3,82 | 3,8 | 3,78 | 3,71 | 3,7 | 3,68 | 3,65 | 3,62 | 3,61 | 3,6 |
ZV
– эквивалентное число зубьев
– коэффициент, учитывающий угол наклона зуба
Проверка прочности зуба при кратковременных перегрузках
Силы, действующие в зацеплении зубчатых колес
В прямозубых передачах возникают две силы:
a) Ft
– окружная сила,
Ft
= 3881
Н
b) Fr
– радиальная сила, направлена по касательной окружности
Таблица 11– Основные параметры цилиндрической передачи
| Межосевое расстояние αW, мм | Диаметры делительных окружностей, мм | Модуль mn , мм | Число зубьев | Передаточное число i | Ширина зубчатого венца, мм | Силы в зацеплении, Н | |
| dш | dк | Zш | Zк | bш | bк | Ft | Fr |
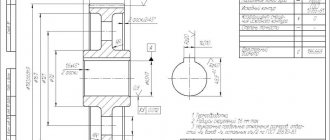
Эскиз зубчатого колеса


Рисунок 9 – Эскиз зубчатого колеса
Результаты расчета геометрии зубчатых колёс
d1
=84
мм
;
d2
=416
мм
.
da
=
d
+2
m
;
da1
=84+6=90
мм
;
da2
=416+6=422
мм
.
df
=
d
−2,5
m
;
df1
=84−7, 5=76, 5
мм
;
df2
=416−7, 5=408, 5
мм
.
bш
=55
мм
;
bк
=50
мм
.
δ
=(2,5÷4)
m
≥7, 5-12
мм
.
dст
=(1,6÷1,8)
dв
lст
=(1,2÷1,5)
dв
De
=
df
−2
δ De
=408,5-20=388,5
мм
;
dотв к
=0,25(
De
−
dст
)
C
=(0,2÷0,3)
δ С=3
÷5
мм;
Dотв
=0,5(
De
+
dст
)4. Первый этап эскизной компоновки редуктора.
Ориентировочный расчет валов
Диаметры валов предварительно определяются из условия прочности на кручение.
для стали 35, 40, 45.
Wp
−полярный момент сопротивления
Диаметр вала округляют до целого числа, оканчивающегося на ноль или пять.
dш
=35
мм
dк
=60
мм.
При выполнении первой эскизной компоновки валы принимаются без ступеней. Подшипники выбираются шариковые, средней серии 300 по диаметру вала.
Построение ведется на миллиметровой бумаге в масштабе один к одному или на компьютере.
Таблица 12 – Шарикоподшипники радиальные однорядные [2] c 394
| Условное обозначение | d | D | B |
|
| 307 312 | 35 60 | 80 130 | 21 31 |
Таблица 13 – Крышки подшипников торцевые или фланцевые
| D | D1 | D2 | D3 | H |
| 50, 52 | ||||
| 50, 58 60, 62 | ||||
| 65, 68 70, 72 | 12 | |||
| 80, 85 90, 98 | 100 | 120 | 72 | |
| 105, 110 | ||||
| 130, 140 | 165 | 190 | 125 | 20 |


Рисунок 11 – Крышки врезные
5. Расчет валов
Данные для расчета валов
Таблица 14 – Параметры, используемые при расчете валов
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 — 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
Общее определение
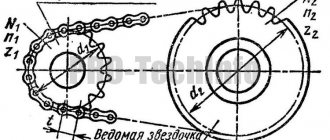
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:
- ременная;
- цепная;
- зубчатая.
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

Переходной конструкцией является ременная зубчатая передача.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.
Модуль – размер между одинаковыми точками двух соседних зубьев.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.


Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.


Виды зубчатых соединений
Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:
- прямозубая;
- косозубая;
- шевронная;
- коническая;
- винтовая;
- червячная.
Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.
Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.
Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.
Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.
В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.

Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях.
У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.
Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.
Многоступенчатые редукторы
Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.
Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.
Uр = U1×U2 × … ×Un;
Где:
Uр – передаточное число редуктора;
U1,2,n – каждой из пар.
Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.


В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.
Редуктор и коробка скоростей
Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.
Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.
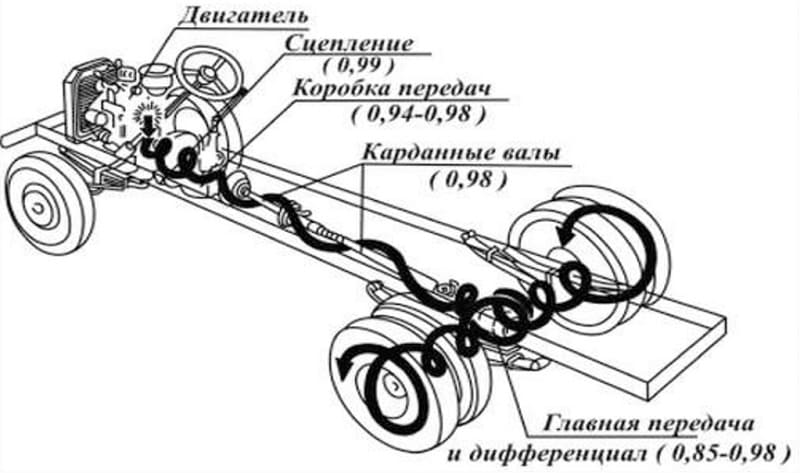
Трансмиссия автомобиля
В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.
В состав трансмиссии входит несколько редукторов. Это, прежде всего:
- коробка передач – скоростей;
- дифференциал.
Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.
Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.


Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.
Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
Окружная скорость колес и степень точности передачи
= 2,8 м/с.
При такой скорости для косозубых колес следует принять 8 степень точности. Для косозубых колес при v
до 10 м/с следует назначать 8-ю степень точности, а свыше 7-ю.
Коэффициент нагрузки
При Ψbd
= 1,473, твердости НВ =< 350 , v = 0,28
м/с
.
КНα
= 1,06;
КНβ
= 1,05;
КНV
= 1,0
Таким образом, коэффициент нагрузки равен: КН
= 1,113.
Проверка контактных напряжений по формуле:
= 372 МПа < [σН].
Силы действующие в зацеплении:
Окружная сила = 1398 Н,
где М1
– вращающий момент на валу зубчатой шестерни.
Радиальная сила = 524 Н.
Здесь угол эвольвентного зубчатого зацепления α = 20о.
Осевая сила = 344 Н.
Проверка зубьев на выносливость по напряжениям изгиба осуществляется по формуле:
Здесь коэффициент нагрузки KF = KFβKFV
При Ψbd
= 1,473, твердости
НВ
=< 350,
V
= 0,28
м/с
.
KFβ
=1,25;
KFV
= 1,1;
Таким образом, коэффициент KF
= 1,2.
YF
– коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев
ZV
У шестерни = 32 мм. => YF
= 3,73.
У колеса = 152 мм. => YF
= 3,60.
Коэффициент Yβ
введен для компенсации погрешности, возникающей из-за применения той же расчетной схемы зуба, что и в случае прямых зубьев. Этот коэффициент определяют по формуле:
= 0,9.
Коэффициент KFα
, учитывает неравномерность распределения нагрузки между зубьями. Для узких зубчатых колес, у которых коэффициент осевого перекрытия
;
коэффициент KFα
принимают равным 1, а иначе этот коэффициент определяется по формуле:
= 092, и так, коэффициент KFα
= 0,92,
где εα
– коэффициент торцевого перекрытия, при учебном проектировании можно принимать среднее значение
εα
= 1,5,
n
– степень точности зубчатых колес.
Допускаемое напряжение находится по формуле:
для Стали 45 улучшенной при твердости НВ =< 350 предел выносливости при нулевом цикле изгиба и коэффициент безопасности [SF]1 = 1,75:
для шестерни = 414 МПа;
для колеса = 360 МПа.
Коэффициент безопасности [SF] определяется как произведение двух коэффициентов:
.
Первый коэффициент [SF]1 учитывает нестабильность свойств материала зубчатых колес. Второй множитель [SF]11 учитывает способ получения заготовки зубчатого колеса: для поковок и штамповок [SF]11 = 1,0; для проката [SF]11 = 1,15; для литых заготовок [SF]11 = 1,3.
Допускаемые напряжения:
для шестерни [σF1]= 237 МПа,
для колеса [σF2]= 206 МПа.
Находим отношение , для шестерни — 64 МПа, для колеса – 57.
Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.
Проверяем прочность зуба колеса
= 92 МПа < [σF2] = 206.
Условие прочности выполнено.
Таблица 4. Результаты расчета
| Наименование | Условное обозна- чение | Ед. изм. | Шестер-ня | Зубчатое колесо |
| Число зубьев | z | |||
| Коэффициент ширины венца | Ψba | 0,45 | ||
| Коэффициент ширины шестерни | Ψbd | 1,473 | ||
| Нормальный модуль зацепления | mn | 1,25 | ||
| Межосевое расстояние | aw | мм | ||
| Делительный диаметр | d | мм | 37,33 | 186,66 |
| Диаметр вершин зубьев | da | мм | 39,83 | 189,16 |
| Диаметр впадин зубьев | df | мм | 34,21 | 183,54 |
| Ширина колеса (шестерни) | b | мм | ||
| Силы действующие в зацеплении: | ||||
| — окружная | Ft | H | 1 398 | |
| — радиальная | Fr | H | ||
| — осевая | Fa | H |
= 2,8 м/с.
При такой скорости для косозубых колес следует принять 8 степень точности. Для косозубых колес при v
до 10 м/с следует назначать 8-ю степень точности, а свыше 7-ю.
Коэффициент нагрузки
При Ψbd
= 1,473, твердости НВ =< 350 , v = 0,28
м/с
.
КНα
= 1,06;
КНβ
= 1,05;
КНV
= 1,0
Таким образом, коэффициент нагрузки равен: КН
= 1,113.
Проверка контактных напряжений по формуле:
= 372 МПа < [σН].
Силы действующие в зацеплении:
Окружная сила = 1398 Н,
где М1
– вращающий момент на валу зубчатой шестерни.
Радиальная сила = 524 Н.
Здесь угол эвольвентного зубчатого зацепления α = 20о.
Осевая сила = 344 Н.
Проверка зубьев на выносливость по напряжениям изгиба осуществляется по формуле:
Здесь коэффициент нагрузки KF = KFβKFV
При Ψbd
= 1,473, твердости
НВ
=< 350,
V
= 0,28
м/с
.
KFβ
=1,25;
KFV
= 1,1;
Таким образом, коэффициент KF
= 1,2.
YF
– коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев
ZV
У шестерни = 32 мм. => YF
= 3,73.
У колеса = 152 мм. => YF
= 3,60.
Коэффициент Yβ
введен для компенсации погрешности, возникающей из-за применения той же расчетной схемы зуба, что и в случае прямых зубьев. Этот коэффициент определяют по формуле:
= 0,9.
Коэффициент KFα
, учитывает неравномерность распределения нагрузки между зубьями. Для узких зубчатых колес, у которых коэффициент осевого перекрытия
;
коэффициент KFα
принимают равным 1, а иначе этот коэффициент определяется по формуле:
= 092, и так, коэффициент KFα
= 0,92,
где εα
– коэффициент торцевого перекрытия, при учебном проектировании можно принимать среднее значение
εα
= 1,5,
n
– степень точности зубчатых колес.
Допускаемое напряжение находится по формуле:
для Стали 45 улучшенной при твердости НВ =< 350 предел выносливости при нулевом цикле изгиба и коэффициент безопасности [SF]1 = 1,75:
для шестерни = 414 МПа;
для колеса = 360 МПа.
Коэффициент безопасности [SF] определяется как произведение двух коэффициентов:
.
Первый коэффициент [SF]1 учитывает нестабильность свойств материала зубчатых колес. Второй множитель [SF]11 учитывает способ получения заготовки зубчатого колеса: для поковок и штамповок [SF]11 = 1,0; для проката [SF]11 = 1,15; для литых заготовок [SF]11 = 1,3.
Допускаемые напряжения:
для шестерни [σF1]= 237 МПа,
для колеса [σF2]= 206 МПа.
Находим отношение , для шестерни — 64 МПа, для колеса – 57.
Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.
Проверяем прочность зуба колеса
= 92 МПа < [σF2] = 206.
Условие прочности выполнено.
Таблица 4. Результаты расчета
| Наименование | Условное обозна- чение | Ед. изм. | Шестер-ня | Зубчатое колесо |
| Число зубьев | z | |||
| Коэффициент ширины венца | Ψba | 0,45 | ||
| Коэффициент ширины шестерни | Ψbd | 1,473 | ||
| Нормальный модуль зацепления | mn | 1,25 | ||
| Межосевое расстояние | aw | мм | ||
| Делительный диаметр | d | мм | 37,33 | 186,66 |
| Диаметр вершин зубьев | da | мм | 39,83 | 189,16 |
| Диаметр впадин зубьев | df | мм | 34,21 | 183,54 |
| Ширина колеса (шестерни) | b | мм | ||
| Силы действующие в зацеплении: | ||||
| — окружная | Ft | H | 1 398 | |
| — радиальная | Fr | H | ||
| — осевая | Fa | H |
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Цилиндрические прямозубые колеса (КПД ~ 90%)
Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.


Червячные передачи (КПД ~ 70%)
Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).


Еще одним преимуществом червячной передачи является то, что у нее только одно направление вращения. Это означает, что только приводной двигатель может вращать такую передачу, в то время как сила тяжести или другие сторонние силы не вызовут каких-либо вращений. Это бывает полезно, например, для стопорения груза на высоте.