Как определить жесткость пружины формула по физике

Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Особенности работы

Любая пружина представляет собой упругое изделие, которое в процессе эксплуатации подвергается статическим, динамическим и циклическим нагрузкам. Основная особенность этой детали – она деформируется под приложенным извне усилием, а когда воздействие прекращается – восстанавливает свою первоначальную форму и геометрические размеры. В период деформации происходит накопление энергии, при восстановлении – ее передача.

Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность.

Виды пружин

Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.

Первые из них без нагрузки имеют нулевой шаг, то есть виток соприкасается с витком. В процессе деформации они растягиваются, их длина увеличивается. Прекращение нагрузки сопровождается возвращением в первоначальную форму – опять витком к витку.
Вторые – наоборот, изначально навиваются с определенным шагом между витками, под нагрузкой сжимаются. Соприкосновение витков является естественным ограничителем для продолжения воздействия.

Изначально именно для пружины растяжения было найдено соотношение массы подвешенного на ней груза и изменения ее геометрического размера, которое и стало основой для формулы жесткости пружины через массу и длину.

Какие еще бывают виды пружин

Зависимость деформации от прилагаемой внешней силы справедлива и для других видов упругих деталей: кручения, изгиба, тарельчатых, других. Не важно, в какой плоскости к ним прилагаются усилия: в той, где расположена осевая линия, или перпендикулярной к ней, производимая деформация пропорциональна усилию, под воздействием которого она произошла.

Модуль Юнга.

В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.

Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать

на величину , то для силы упругости справедлива формула:

Здесь — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.

Звоните нам (бесплатный звонок по России) (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Основные характеристики

Независимо от вида пружин, особенности их работы, связанные с постоянно деформацией, требуют наличия таких параметров:

Способности сохранять постоянное значение упругости в течение заданного срока.
Пластичности.
Релаксационной стойкости, благодаря которой деформации не становятся необратимыми.
Прочности, то есть способности выдерживать различные виды нагрузок: статические, динамические, ударные.

Каждая из этих характеристик важна, однако при выборе упругой комплектующей для конкретной работы в первую очередь интересуются ее жесткостью как важным показателем того, подойдет ли она для этого дела и насколько долго будет работать.

Что такое жесткость

Жесткость – это характеристика детали, которая показывает, просто или легко будет ее сжать, насколько большую силу нужно для этого приложить. Оказывается, что возникающая под нагрузкой деформация тем больше, чем больше прилагаемая сила (ведь возникающая в противовес ей сила упругости по модулю имеет то же значение). Потому определить степень деформации можно, зная силу упругости (прилагаемое усилие) и наоборот, зная необходимую деформацию, можно вычислить, какое требуется усилие.

Физические основы понятия жесткость/упругость

Сила, воздействуя на пружину, изменяет ее форму. Например, пружины растяжения/сжатия под влиянием внешнего воздействия укорачиваются или удлиняются. Согласно закону Гука (так называется позволяющая рассчитать коэффициент жесткости пружины формула), сила и деформация между собой пропорциональны в пределах упругости конкретного вещества. В противодействие приложенной извне нагрузке возникает сила, такая же по величине и противоположная по знаку, которая направлена на восстановление исходных размеров детали и ее форму.

Природа этой силы упругости – электромагнитная, возникает она как следствие особого взаимодействии между структурными элементами (молекулами и атомами) материала, из которого изготовлена данная деталь. Таким образом, чем жесткость больше, то есть чем труднее упругую деталь растянуть/сжать, тем больше коэффициент упругости. Этот показатель используется, в частности, при выборе определенного материала для изготовления пружин для использования в различных ситуациях.

Подписи к слайдам:

Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М.В.

проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование: набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.

Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?

Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.

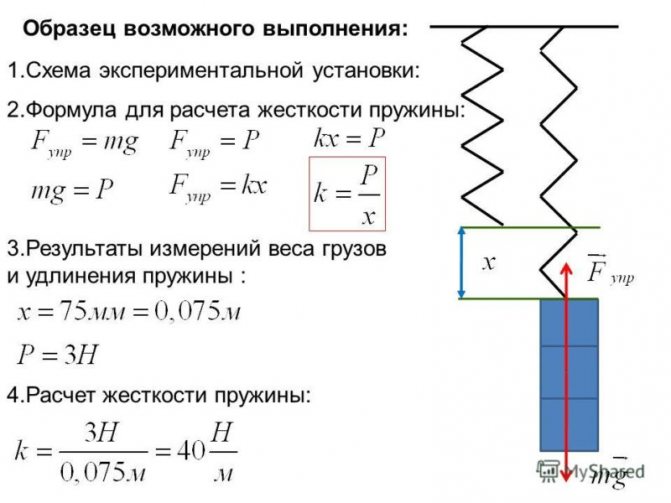
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х, можно найти коэффициент жесткости k по формуле

В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:

№ опыта m, кг mg, H х, м 1 0,1 2 0,2 3 0,3 4 0,4

6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср. 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10. Запишите сделанный вами вывод.

Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.

Разработки уроков (конспекты уроков)

Среднее общее образование

Линия УМК Г. Я. Мякишева. Физика (10-11) (У)

Внимание! Администрация сайта сайт не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС. Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины, рассчитать погрешность измерения величины

Цель урока:

проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины, рассчитать погрешность измерения величины.

Задачи урока:

образовательные: умение обрабатывать и объяснять результаты измерений и делать выводы Закрепление экспериментальных умений и навыков
воспитательные: вовлечение учащихся в активную практическую деятельность, совершенствование навыки общения.
развивающие: владение основными приемами, используемыми в физике – измерение, эксперимент

Тип урока:

урок обучения умениям и навыкам

Оборудование:

штатив с муфтой и зажимом, винтовая пружина, набор грузиков известной массы (по 100 г, погрешность Δm = 0,002 кг), линейка с миллиметровыми делениями.

Как появился первый вариант формулы

Формула для расчета жесткости пружины, которая получила название закона Гука, была установлена экспериментально. В процессе опытов с подвешенными на упругом элементе грузами разной массы замерялась величина его растяжения. Так и выяснилось, что одна и та же испытуемая деталь под разными нагрузками претерпевает различные деформации. Причем подвешивание определенного количества гирек, одинаковых по массе, показало, что каждая добавленная/снятая гирька увеличивает/уменьшает длину упругого элемента на одинаковую величину.

В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).

Так было открыто свойство жесткости, которое, как и формула для определения коэффициента упругости, находит самое широкое применение в любой отрасли промышленности.

Жесткость в физике обозначение

В разделе Домашние задания на вопрос какой буквой обозначается пружина в физике заданный автором Европейский лучший ответ это Нет обозначения пружина, жесткость -К

Привет! Вот подборка тем с ответами на Ваш вопрос: какой буквой обозначается пружина в физике

Ответ от Простофиля Я знаю, что жесткость пружины обозначается «к», а пружина…

Ответ от YOUGOOOOY коэффициент жёсткости — k

Ответ от Игорь Казанжи к

Коэффициент упругости на Википедии Посмотрите статью на википедии про Коэффициент упругости

Список обозначений в физике на Википедии Посмотрите статью на википедии про Список обозначений в физике

Список персонажей телесериала «Стрела» на Википедии Посмотрите статью на википедии про Список персонажей телесериала «Стрела»

Пружины подвески любого транспортного средства выполняют немало важных функций. Правильно подобранные, они оказывают качественное влияние на весь процесс управления автомобилем и его грузоподъемность, делают неровности дорожного покрытия менее заметными для водителя, повышают комфорт при поездках, особенно длительных.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

Читать также: Разработка технологического процесса сварки

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

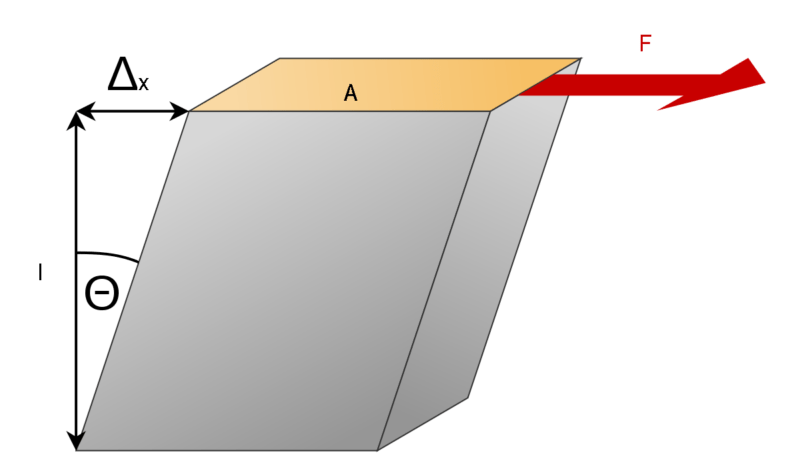
Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

Материала, используемого при ее изготовлении.
Формы и конструктивных особенностей.
Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

Опытный метод

Чтобы понять, как найти жесткость пружины, а точнее, определить коэффициент жесткости пружины опытным путем, следует произвести следующие манипуляции. Вам необходимо деформировать тело, прилагая к нему силу. Самый простой вид деформации – это сжатие или растяжение. Коэффициент жесткости показывает именно то, какую силу необходимо приложить к телу, чтобы упруго деформировать его на единицу длины. Мы сейчас говорим об упругой деформации, когда тело принимает свою первоначальную форму после совершения воздействия на него. Для того чтобы провести этот наглядный эксперимент вам потребуются следующие вещи:

калькулятор,
ручка,
тетрадь,
пружина,
линейка,
груз.

Итак, один конец пружины закрепите вертикально, а второй оставьте свободным. Измерьте длину пружины и запишите результат в тетрадь (это будет значение x1). Подвесьте к свободному концу пружины груз весом в сто граммов и опять измерьте длину пружины, запишите значение (x2). Рассчитайте абсолютное удлинение пружины (разница значений x1 и x2). При небольших сжатиях и растяжениях сила упругости пропорциональна деформации. Здесь уже применяем Закон Гука, согласно которому Fупр = |kx|, где k и является коэффициентом жесткости. Для того чтобы найти нужный нам коэффициент жесткости надо силу растяжения разделить на удлинение пружины. Силу растяжения находим следующим образом: Fупр = – N = -mg. Отсюда следует, что mg = kx. А значит, k = mg/x. Дальше все просто: подставьте известные вам значения в формулу и найдите, чему равна жёсткость пружины.

Если под воздействием внешних сил на твердое тело оно деформируется, то в нем происходят смещения частиц узлов кристаллической решетки. Этому сдвигу противостоят силы взаимодействия частиц. Так возникают силы упругости, которые приложены к телу, подвергшемуся деформации. Модуль силы упругости пропорционален деформации:

где — напряжение при упругой деформации, K — модуль упругости, который равен напряжению при относительной деформации, равной единице. где — относительная деформация, — абсолютная деформация, — первоначальное значение величины, которая характеризовала форму или размеры тела.

ОПРЕДЕЛЕНИЕ

Коэффициентом упругости

называют физическую величину, которая связывает в законе Гука удлинение, возникающее при деформации упругого тела и силу упругости. Величина равная называется коэффициентом упругости. Она показывает изменение размера тела под воздействием нагрузки при упругой деформации.

Коэффициент упругости зависит от материала тела, его размеров. Так при увеличении длины пружины и уменьшении ее толщины коэффициент упругости уменьшается.

Особенности расчета жесткости соединений пружин

Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.

При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.

При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.

Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.

Пружина – упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип – запасать энергию упругой деформации и возвращать ее.

Попробуй обратиться за помощью к преподавателям

Что зависит от упругости пружины

Без такого элемента не обходится ни один механизм или прибор. Они применяются и при изготовлении мебели.

Их можно обнаружить в транспортных средствах, в станках, дверных замках и ручках, диванах, матрацах, часах, шариковых ручках и т. д. Где бы ни устанавливалась спираль из проволоки, её работа оказывает решающее влияние на функционирование механизма (изделия).

Так, если она очень жёсткая или мягкая, то установленная в автомобильном амортизаторе не будет способствовать комфортной и безопасной езде по неровной дороге, а если встроена в мебель, то сидеть и лежать на ней будет не очень приятно.

Физические характеристики пружин

Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость – способность сопротивляться деформации:

материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Задай вопрос специалистам и получи ответ уже через 15 минут!

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.

Понятие жесткости

Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.

Читать также: Холодильник индезит постоянно работает не отключается

Коэффициент жесткости рассчитывается по формуле Гука:

где $F$ – сила, развиваемая пружиной, $k$ – коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ – абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.

Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость

$m cdot g – k cdot x = 0$,

где $m$ – масса, $g$ – ускорение свободного падения. Отсюда

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину $\Delta L$. Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

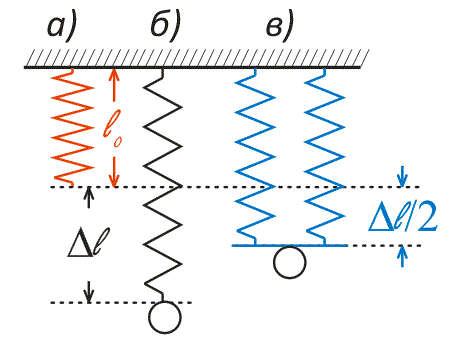
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две параллельные пружины:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{параллел}} \cdot \frac{1}{2}= k_{1} \]

Умножим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{параллел}} = 2k_{1} } \]

Коэффициент жесткости $k_{\text{параллел}}$ двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину $\Delta L$. Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину $\Delta L$.

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

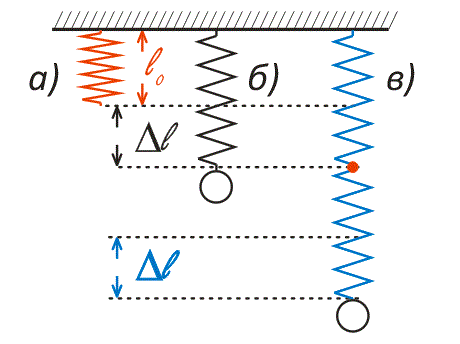
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две последовательные пружины:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{послед}} \cdot 2 = k_{1} \]

Разделим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{послед}} = \frac{k_{1}}{2} } \]

Коэффициент жесткости $k_{\text{послед}}$ двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$R$ — радиус цилиндра пружины,
$n$ — количество витков проволоки радиуса $r$,
$G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^<10>$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков – 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac<�Н><�м>$

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

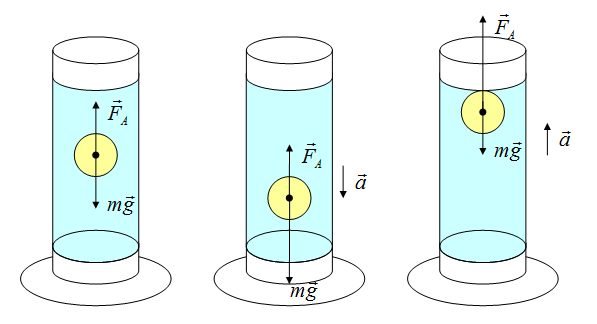
Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как Сила Кулона, сила Ампера, сила Лоренца.

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Локальная система отсчёта

— это система отсчёта, которая может считаться инерциальной, но лишь в бесконечно малой окрестности какой-то одной точки пространства-времени, или лишь вдоль какой-то одной незамкнутой мировой линии.

Преобразования Галилея. Принцип относительности в классической механике.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система Kбудет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+vt;y=y’;z=z’;t=t’, названных преобразованиями Галилея.Механический принцип относительности.Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.Нарушение классического закона сложения скоростей.Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x’=(x-vt)/(1-v 2 /c 2 ); y’=y; z’=z; t’=(t-vx/c 2 )/(1-v 2 /c 2 ). Эти преобразования называются преобразованиями Лоуренса.

Определение и формула жесткости пружины

При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:

Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.

Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.

Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:

Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.

Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd 4 /8D 3 n. В этой формуле указываются нижеприведенные обозначения:

G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.

Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.

Формула жесткости соединений пружин

Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:

Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.

Читать также: Чем обезжирить дверь перед покраской

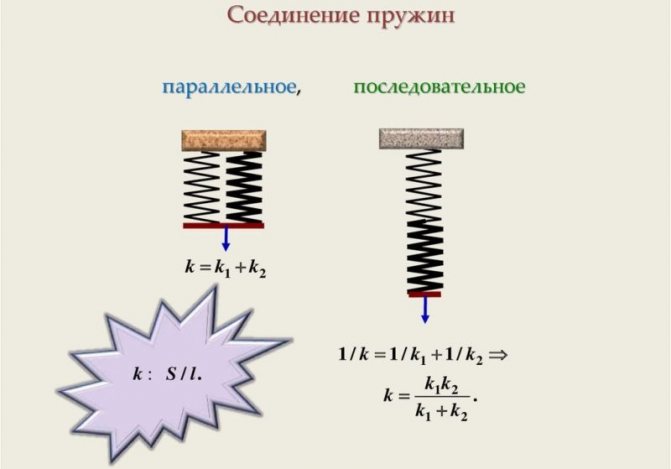
В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.

При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k1+1/k2+…+1/kn. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k1+k2+…kn.

Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.

Коэффициент жесткости соединений пружин

Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:

При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.

Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Коэффициент жесткости цилиндрической пружины

На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:

При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.

Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:

Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.

Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:

Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
Модуля сдвига, который зависит от типа применяемого материала.

Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.

Единицы измерения

При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.

Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.

Разделение пружины по цветам проводится в сфере автомобилестроения.

Среди особенностей подобной маркировки отметим следующее:

Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
Класса В представлен синим, голубым, черным и желтым цветом.

Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.