Что такое поперечное сечение цилиндра?

Навигация по странице:Определение цилиндраЭлементы цилиндраКруговой цилиндрОбъём кругового цилиндраПлощадь поверхности кругового цилиндраКосой цилиндрНаклонный цилиндрОпределение.Цилиндр

— это геометрическое тело, ограниченное
цилиндрической поверхностью
и двумя плоскостями (
основами цилиндра
).
Цилиндрическая поверхность
— поверхность, получаемая при движении прямой (
образующей L
) параллельно самой себе, вдоль плоской кривой
направляющей
.
Основания цилиндра
– плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Рис. 1

Рис. 2

Рис. 3

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

Определение объемов емкостей.
Решение задач по сопротивлению материалов и электротехнике.
Расчет количества материалов при проектировании, строительстве и ремонте.
Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
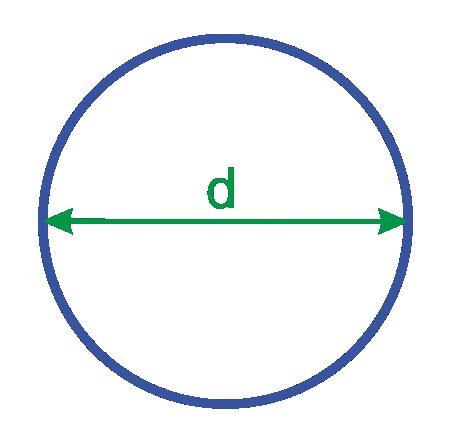
диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Непростая задача о площади сечения цилиндра, которая может ввести в заблуждение.

Диаметр основания цилиндра равен 8, а длина его образующей – . На окружности верхнего основания цилиндра выбраны точки F и D, делящие окружность на две дуги, длины которых относятся как 1:2. Найдите площадь сечения цилиндра плоскостью, проходящей через точки F, D и центр нижнего основания. На первый взгляд – задача простая. Кажется, что сечение – трапеция, нижнее ее основание – диаметр цилиндра, найти длину верхнего основания вполне можно, также возможно отыскать высоту трапеции и – дело в шляпе. Однако..

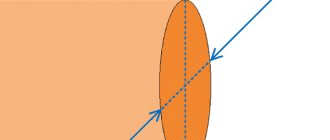
Однако надо помнить, что сечение цилиндра наклонной плоскостью – всегда эллипс или его часть!

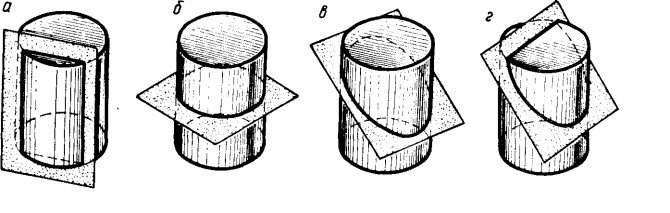
Сечения цилиндра

Посмотрим на различные сечения цилиндра плоскостями:

Наш случай приблизительно такой:

Сечение цилиндра неосевой плоскостью

И еще нам потребуется знать, какой будет проекция этого сечения на основание цилиндра:

Проекция сечения

Проекция – вид сверху

Все дело в том, что рассчитать непосредственно площадь сечения трудно из-за сложности его формы, поэтому воспользуемся тем, что

Площадь проекции плоской фигуры равна произведению площади этой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции.

Проекция – вид сверху

Определить площадь проекции будет несложно, давайте это сделаем. Проекция будет представлять собой часть полукруга, которую можно разбить на два круговых сектора и треугольник. Нам известно, что длины дуг относятся как 1:2, значит, меньшая дуга имеет градусную меру , и ей соответствует центральный угол с такой же градусной мерой, который является одним из углов треугольника FDC. Тогда, поскольку треугольник этот – равнобедренный, то два его острых угла равны , а высота будет равна половине радиуса цилиндра (против угла в лежит катет, вдвое меньший гипотенузы). Определим основание треугольника FDC, для этого найдем его половину по теореме Пифагора: , где FC – радиус цилиндра, FC=4,

Площадь треугольника FDC равна половине произведения основания на высоту:

Кроме треугольника FDC в состав площади проекции сечения входят еще два круговых сектора, центральные углы которых равны 30, то есть площадь каждого из них – 1/12 часть круга, а вместе их площадь – 1/6 часть круга, или . Площадь проекции: .

Осталось определить . Сделаем еще рисунок:

Найдем высоту сечения, это гипотенуза треугольника KGO, KO: . В этом выражении нам все известно: KG – это высота – h, а GO – это образующая цилиндра, его высота. Тогда

Косинус нужного угла – отношение прилежащего катета к длине гипотенузы:

Сечение. Вид сбоку

Тогда искомая площадь:

Объем правильного цилиндра через радиус и высоту цилиндра

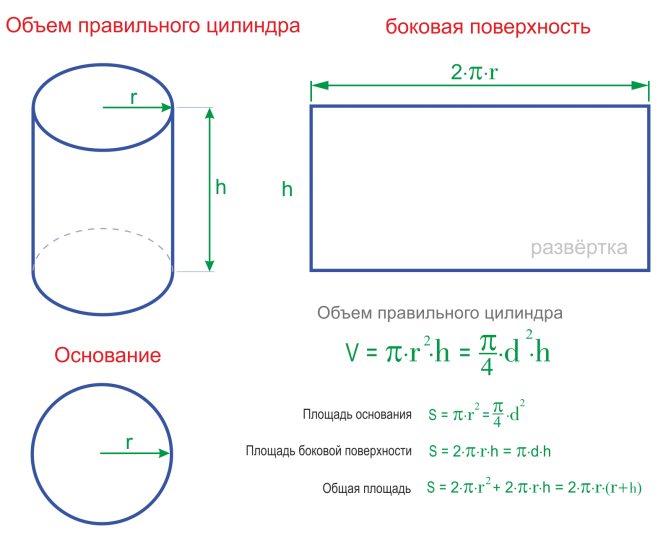
r — радиус основания цилиндра
h — высота цилиндра

… вычисление …

Упрощение формулы:

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

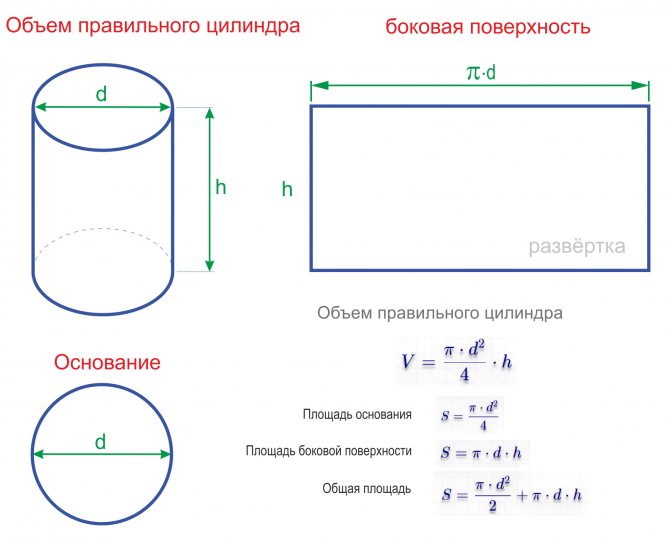
d — диаметр основания цилиндра

h — высота цилиндра

… вычисление …

Формула площади поверхности наклонного кругового цилиндра

S осн = 2 ⋅ π ⋅ r 2 S_{\text{осн}}=2\cdot\pi\cdot r^2 Sосн=2⋅π⋅r2

S бок = p ⋅ l S_{\text{бок}}=p\cdot l Sбок=p⋅l

r r r — радиус круга (основания кругового цилиндра); p p p — периметр сечения наклонного цилиндра перпендикулярно образующей; l l l — длина образующей этого цилиндра.

Пример

Найти площадь поверхности наклонного цилиндра, если периметр p p p сечения плоскости, составляющей прямой угол с образующей, равен 30 (см.), а сама образующая равна 7 (см.) Радиус окружности, лежащей в основе цилиндра в два раза меньше его образующей.

Решение:

r = l 2 r=\frac{l}{2} r=2l p = 30 p=30 p=30 l = 7 l=7 l=7

Найдем сначала радиус основания:

r = l 2 = 7 2 = 3.5 r=\frac{l}{2}=\frac{7}{2}=3.5 r=2l=27=3.5

Тогда полная площадь:

S = S осн + S бок = 2 ⋅ π ⋅ r 2 + p ⋅ l = 2 ⋅ π ⋅ 3. 5 2 + 30 ⋅ 7 ≈ 76 , 93 + 210 = 286 , 93 S=S_{\text{осн}}+S_{\text{бок}}=2\cdot\pi\cdot r^2+p\cdot l=2\cdot\pi\cdot 3.5^2+30\cdot 7\approx76,93+210=286,93 S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93 (см. кв.)

Ответ: 286,93 см. кв.

На сайте Студворк предусмотрено решение контрольных работ на заказ для школьников и студентов.

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью. Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

Рис.3

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Рис.4

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

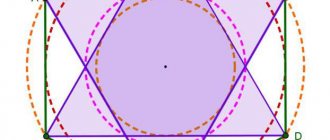
Как связан цилиндр с вписанной в него или описанной около него призмой?

Иногда встречаются задачи, в которых нужно вычислить площадь цилиндра, а известны при этом некоторые элементы связанной с ним призмы. Как соотносятся эти фигуры?

Если призма вписана в цилиндр, то ее основания – равные многоугольники. Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.

У описанной призмы в основаниях находятся правильные многоугольники. Они описаны около кругов цилиндра, являющихся его основаниями. Плоскости, которые содержат грани призмы, касаются цилиндра по образующим.

Виды цилиндра

Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.

Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.

Если угол другой, то цилиндр называется наклонным.

Если форма основания – гипербола, то цилиндр гиперболический, если парабола — параболический, если эллипс — эллиптический, если круг — круговой.

Если основания цилиндра не параллельны, то он называется косым.

Примеры задач

Задание 1 Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение: Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения: S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2 Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение: Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем: S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Источник

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

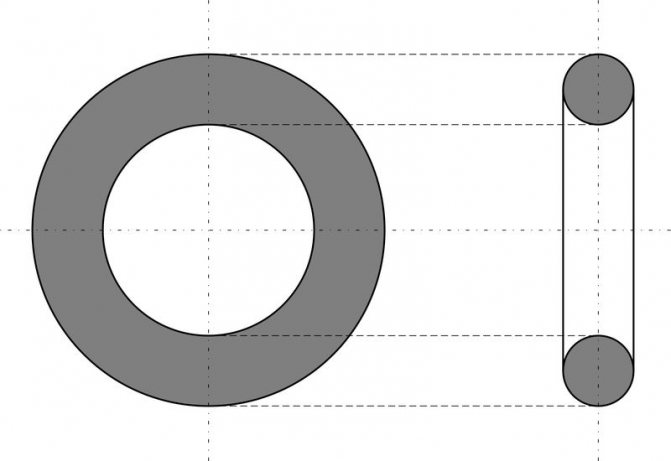
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Цилиндр – это геометрическая фигура, полученная вращением прямоугольника вокруг одной из его сторон. У каждого цилиндра есть 2 одинаковых основания (верхнее и нижнее) и боковая поверхность.

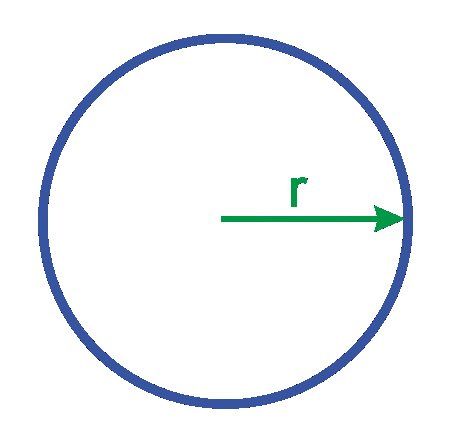
Любой цилиндр характеризуется высотой h (осевой линией) и радиусом r (см. рисунок). Именно эти характеристики используются в формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.

Высота цилиндра (осевая линия) – это перпендикуляр, проведенный от верхнего основания к нижнему.

Радиус цилиндра – это радиус его основания.

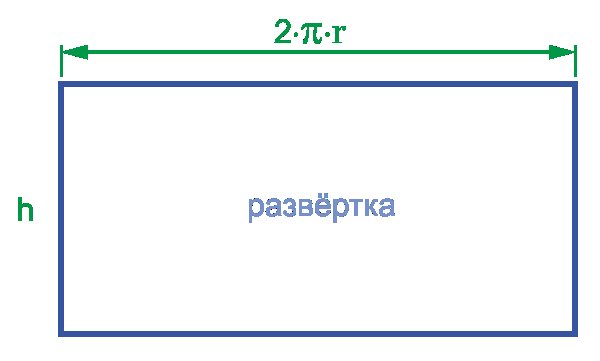
Площадь боковой поверхности цилиндра можно получить, зная его высоту H и длину основания L:

Sбок.пов = LH = 2πrH

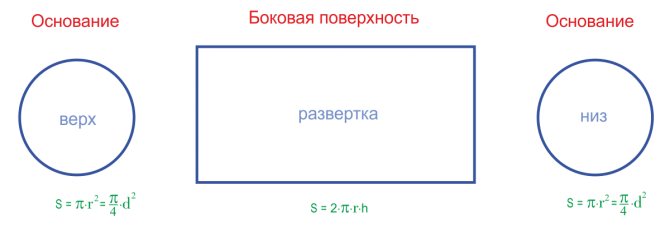
Формула площади поверхности кругового цилиндра

S осн = 2 ⋅ π ⋅ r 2 S_{\text{осн}}=2\cdot\pi\cdot r^2 Sосн=2⋅π⋅r2

S бок = 2 ⋅ π ⋅ r ⋅ h S_{\text{бок}}=2\cdot\pi\cdot r\cdot h Sбок=2⋅π⋅r⋅h

r r r — радиус круга (основания кругового цилиндра); h h h — высота этого цилиндра.

Сокращенно, это формулу можно записать так:

S = S осн + S бок = 2 ⋅ π ⋅ r 2 + 2 ⋅ π ⋅ r ⋅ h = 2 ⋅ π ⋅ r ⋅ ( r + h ) S=S_{\text{осн}}+S_{\text{бок}}=2\cdot\pi\cdot r^2+2\cdot\pi\cdot r\cdot h=2\cdot\pi\cdot r\cdot(r+h) S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)

Пример

Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.

Решение:

r = 6 r=6 r=6 h = 20 h=20 h=20

По формуле:

S = 2 ⋅ π ⋅ r ⋅ ( r + h ) = 2 ⋅ π ⋅ 6 ⋅ ( 6 + 20 ) ≈ 979 , 68 S=2\cdot\pi\cdot r\cdot(r+h)=2\cdot\pi\cdot 6\cdot(6+20)\approx979,68 S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68 (см. кв.)

Ответ: 979,68 см. кв.