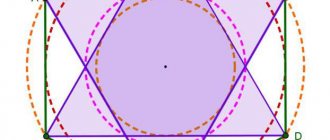
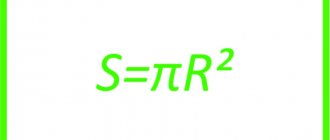Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда . После того, как найдем диагональ – мы сможем рассчитать радиус: . И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата. Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности. Для начала рассчитаем длину диагонали d. Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Таблица соответствия диаметров проводов и их площадь сечения
Проводить расчеты в магазине или на рынке не всегда хочется или есть возможность. Чтобы не тратить время на расчеты или не ошибиться, можно воспользоваться таблицей соответствия диаметров и сечений проводов, в которой есть наиболее распространенные (нормативные) размеры. Ее можно переписать, распечатать и захватить с собой.
| Диаметр проводника | Сечение проводника |
| 0,8 мм | 0,5 мм2 |
| 0,98 мм | 0,75 мм2 |
| 1,13 мм | 1 мм2 |
| 1,38 мм | 1,5 мм2 |
| 1,6 мм | 2,0 мм2 |
| 1,78 мм | 2,5 мм2 |
| 2,26 мм | 4,0 мм2 |
| 2,76 мм | 6,0 мм2 |
| 3,57 мм | 10,0 мм2 |
| 4,51 мм | 16,0 мм2 |
| 5,64 мм | 25,0 мм2 |
Как работать с этой таблицей? Как правило, на кабелях есть маркировка или бирка, на которой указаны его параметры. Там указывается маркировка кабеля, количество жил и их сечение. Например, ВВНГ 2х4. Нас интересуют параметры жилы а это цифры, которые стоят после знака «х». В данном случае заявлено, что есть два проводника, имеющих поперечное сечение 4 мм2. Вот и будем проверять, соответствует ли эта информация действительности.
Как работать с таблицей
Чтобы проверить, проводите измерение диаметра любым из описанных методов, после сверяетесь с таблицей. В ней указано, что при таком сечении в четыре квадратных миллиметра, размер провода должен быть 2,26 мм. Если измерения у вас такие же или очень близкие (погрешность измерений существует, так как приборы неидеальные), все нормально, можно данный кабель покупать.

Заявленные размеры далеко не всегда соответствуют реальным
Но намного чаще фактический диаметр проводников значительно меньше заявленного. Тогда у вас два пути: искать провод другого производителя или взять большего сечения. За него, конечно, придется переплатить, но первый вариант потребует достаточно большого промежутка времени, да и не факт, что вам удастся найти соответствующий ГОСТу кабель.
Второй вариант потребует больше денег, так как цена существенно зависит от заявленного сечения. Хотя, не факт — хороший кабель, сделанный по всем нормам, может стоит еще дороже. Это и понятно — расходы меди, а, часто, и на изоляцию, при соблюдении технологии и стандартов — значительно больше. Потому производители и хитрят, уменьшая диаметр проводов — чтобы снизить цену. Но такая экономия может обернуться бедой. Так что обязательно проводите измерения перед покупкой. Даже и проверенных поставщиков.
И еще: осмотрите и пощупайте изоляцию. Она должна быть толстой, сплошной, иметь одинаковую толщину. Если кроме изменения диаметра еще и с изоляцией проблемы — ищите кабель другого производителя. Вообще, желательно найти продукцию, отвечающую требованиям ГОСТа, а не сделанную по ТУ. В этом случае есть надежда на то, что кабель или провод буде служить долго и без проблем. Сегодня это сделать непросто, но если вы разводите проводку в доме или подключаете электричество от столба, качество очень важно. Потому, стоит, наверное, поискать.
Вычисление сечения провода для линии розеток
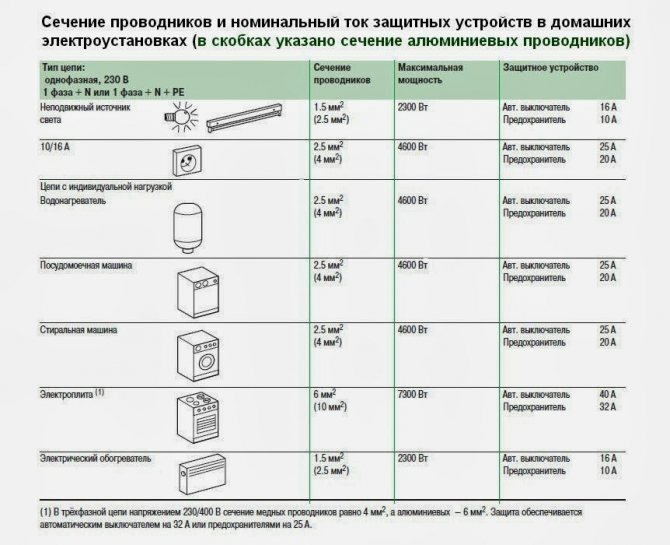

Сечение кабелей для домашних электроустановок
Каждый электроприбор имеет показатели собственной мощности. Они замеряются в Ваттах и указываются в паспорте либо на наклейке на корпусе. Примером поиска сечения будет линия запитки для стиральной машины мощностью 2,4 кВт. При расчетах учитывается:
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.
Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Математика ЕГЭ
Информатика ЕГЭ
Алексей Шевчук — ведущий курсов
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — 19 лет (c 2003 года);
- в 2022 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Выбор толщины провода и автоматического выключателя, исходя из потребляемой мощности и тока
Ниже – таблица выбора сечения провода, исходя из известной мощности или тока. А в правом столбце – выбор автоматического выключателя, который ставится в этот провод.
Таблица 2
| Макс. мощность, кВт | Макс. ток нагрузки, А | Сечение провода, мм2 | Ток автомата, А |
| 1 | 4.5 | 1 | 4-6 |
| 2 | 9.1 | 1.5 | 10 |
| 3 | 13.6 | 2.5 | 16 |
| 4 | 18.2 | 2.5 | 20 |
| 5 | 22.7 | 4 | 25 |
| 6 | 27.3 | 4 | 32 |
| 7 | 31.8 | 4 | 32 |
| 8 | 36.4 | 6 | 40 |
| 9 | 40.9 | 6 | 50 |
| 10 | 45.5 | 10 | 50 |
| 11 | 50.0 | 10 | 50 |
| 12 | 54.5 | 16 | 63 |
| 13 | 59.1 | 16 | 63 |
| 14 | 63.6 | 16 | 80 |
| 15 | 68.2 | 25 | 80 |
| 16 | 72.7 | 25 | 80 |
| 17 | 77.3 | 25 | 80 |
Красным цветом выделены критические случаи, в которых лучше перестраховаться и не экономить на проводе, выбрав провод потолще, чем указано в таблице. А ток автомата – поменьше.
Глядя в табличку, можно легко выбрать сечение провода по току, либо сечение провода по мощности.
А также – выбрать автоматический выключатель под данную нагрузку.
В этой таблице данные приведены для следующего случая.
- Одна фаза, напряжение 220 В
- Температура окружающей среды +30 0С
- Прокладка в воздухе или коробе (в закрытом пространстве)
- Провод трехжильный, в общей изоляции (кабель)
- Используется наиболее распространенная система TN-S с отдельным проводом заземления
- Достижение потребителем максимальной мощности – крайний, но возможный случай. При этом максимальный ток может действовать длительное время без отрицательных последствий.
Если температура окружающей среды будет на 20 0С выше, или в жгуте будет несколько кабелей, то рекомендуется выбрать большее сечение (следующее из ряда). Особенно это касается тех случаев, когда значение рабочего тока близко к максимальному.
Вообще, при любых спорных и сомнительных моментах, например
- возможное в будущем увеличение нагрузки
- большие пусковые токи
- большие перепады температур (электрический провод на солнце)
- пожароопасные помещения
нужно либо увеличивать толщину проводов, либо более детально подойти к выбору – обратиться к формулам, справочникам. Но, как правило, табличные справочные данные вполне пригодны для практики.
Толщину провода можно узнать не только из справочных данных. Существует эмпирическое (полученное опытным путем) правило:
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
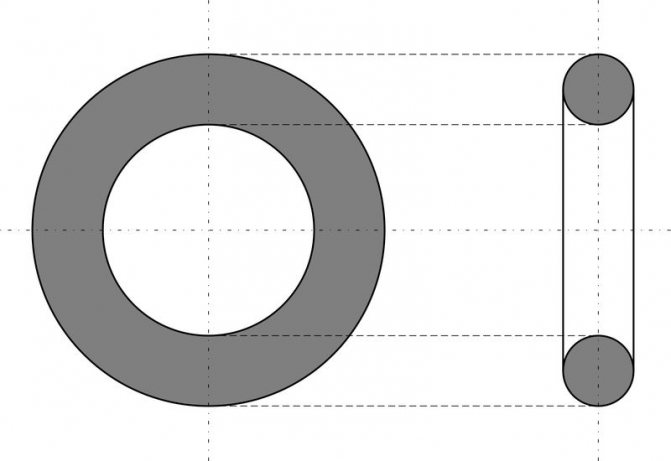
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Источники
- https://tokar.guru/hochu-vse-znat/raschet-ploschadi-poperechnogo-secheniya-kruga.html
- https://mnogoformul.ru/formuly-ploshhadi-kruga-i-raschet-onlayn
- https://www.calc.ru/ploshchad-kruga.html
- https://ru.onlinemschool.com/math/formula/circle/
- https://allcalc.ru/node/18
- https://minus-procentov-online.ru/krug/diametr/
- https://doza.pro/art/math/geometry/area-circle
- https://zen.yandex.ru/media/studystudent/dlina-okrujnosti-i-ploscad-kruga-formuly-i-primery-5e9d7c122517bd2ed0b40460
- https://2mb.ru/matematika/geometriya/ploshhad-kruga/
Таблица с формулами площади круга
| Радиус круга r | |
| Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно | |
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | радиус | |
| 2 | диаметр | |
| 3 | длина окружности | |
| 4 | сторона квадрата вписанного в круг | |
| 5 | сторона квадрата, в который вписан круг | |
| 6 | стороны треугольника | где |
| 7 | сторона равностороннего треугольника | |
| 8 | высота равностороннего треугольника | |
| 9 | боковая сторона и основание равнобедренного треугольника | |
| 10 | стороны при прямом угле треугольника | |
| 11 | боковая сторона и основание равнобедренного треугольника | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними | |
| 13 | стороны прямоугольного треугольника | |
| 14 | сторона и угол при основании треугольника | |
| 15 | сторона равностороннего треугольника | |
| 16 | сторона и угол при основании трапеции | |
| 17 | боковые стороны и диагональ трапеции | где |
| 18 | стороны прямоугольника | |
| 19 | сторона и количество сторон многоугольника | |
| 20 | сторона шестиугольника |
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство: