Использование формулы массы через плотность и объём

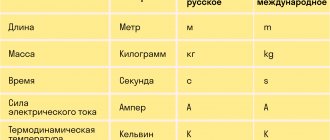
Физика — наука невероятно увлекательная, если разобраться, что там к чему. А формулы в ней отражают реальные физические процессы, только в цифрах. И если вы будете понимать, почему формула именно такова, то учиться будет много легче. Но все сразу рассказать невозможно, и сегодня мы разберемся, как произвести нахождение массы через плотность и объём.

Прежде, чем приступить к изучению формул массы, плотности и объёма, следует уточнить некоторые детали:

• Во-первых, объём вещества зависит от температуры. При нагревании твёрдое вещество расширяется, при низкой температуре уменьшается. Есть также особые моменты, как в случае с жидким водородом. Он не может существовать при высокой температуре, потому что превратится в газ.
• Во-вторых, разные организации и страны имеют свои стандарты условий, при которых проводятся измерения. Иными словами, числовой показатель плотности одного и того же вещества в разных странах будет отличаться. Поэтому, прежде чем утверждать, что показатели неверные или правильные, следует уточнить условия, при которых эти показатели были получены.
• В-третьих, помимо температуры, на фактор объёма могут влиять и такие показатели, как атмосферное давление. Оно особо важно при измерении плотности газов, так как на твёрдые вещества это практически не влияет.

Формула и удивительная история её возникновения

Самая обычная формула для большинства случаев имеет вид: m = pV , где m – масса тела, p и V – плотность вещества и его объём, занимаемый в пространстве соответственно. Можно, конечно, не заморачиваться и посчитать всё на онлайн-ресурсах, но знать формулу всё же полезно. Соответственно V = m / p , p = m / V .

Самое интересное – это то, что формулу нашёл мужик, который бегал голышом по улице и был при этом другом царя. Интересно? Тогда следующие три абзаца для вас.

Был в Древней Греции такой царь-тиран, как Гиерон II. Он начал подозревать, что его корону сделали не из чистого золота и ювелиры его облапошили. Но Гиерон не знал, как можно это доказать. Тогда он обратился к умнейшему человеку того времени – Архимеду. Получив приказ разобраться с делами государственной важности, Архимед день за днём стал искать решение вопроса.

Ох, и нелёгкая же задачка выпала учёному. Ведь на то время не было ни нужных формул, ни современных девайсов, ни гугла, чтобы быстренько найти решение. И вот однажды, придя в баню и погрузившись в неё, Архимед заметил, что выливающаяся вода равна по объёму тому, что погружено в воду.

Эврика! – Прокричал Архимед и нагишом поспешил в свою лабораторию проводить опыты. Учёный сложил все данные в своей голове и позже проделал следующий опыт: он взял корону и опустил её в воду. Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.

Масса сплошной детали

Главная > Вычисление масс > Масса сплошной детали

9.05.2013 // Владимир Трунов

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:

Масса цилиндра

Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:

Масса шара

Объем шара: , где — диаметр шара. Тогда масса:

Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:

Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:

Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:

Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:

Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

вычисление массы

Похожие записи

• Масса кольца, звена

• Масса обручального кольца

• Масса проволоки, прутка, проката

Обозначения и термины

Далее будет приведён список понятий и их определение в условиях понятий об измерениях плотности:

• Масса – плотность тела, помноженная на его объём, занимаемый в пространстве. Это также величина, определяющая силу воздействия гравитационного поля на объект.
• Объём – физическая величина, характеризующая количество пространства, занимаемое объектом.
• Плотность определяет то, какое количество вещества умещается в объёме при определённом весе в стандартных условиях.
• Нормальные/стандартные условия в разных организациях имеют свои значения. К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры.
• Атмосферное давление – понятие, применяемое больше для газов, так как на их объём имеет большое влияние, нежели на твёрдые вещества. Атмосферное давление можно определить как силу, с которой воздействует воздух на Землю под действием гравитационного поля.
• Температура – физический показатель степени нагрева вещества. Чем больше температура, тем больше объём тела.

Особенности

В случае с пористыми либо сыпучими субстанциями (к первым относится, например, ракушечник, ко вторым – крупы, из которых готовятся каши) различают две плотности:

• истинную – с вычетом пустот, заполненных воздухом либо жидкостью;
• насыпную – определяется описанным выше способом, когда в объём пористого/сыпучего материала входят пустоты.

Реальную плотность вычисляют из кажущейся (насыпной) через определённый на практике коэффициент – исключает пустоты.

С ростом температуры плотность вещества снижается, хотя есть исключения, например, вода. При 4 °C она наиболее плотная, при охлаждении и нагреве значение снижается, причём лёд легче воды в жидком состоянии.

Примеры решения задач

Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.

Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.

Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.

Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.

Расчет массы тела по его плотности

Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.

Плотность определяется по формуле $\rho = \frac{m}{V}$. Выразим отсюда массу:

$$m = \rho V$$

Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.

Рассмотрим пример задачи на расчет массы. Рассчитайте массу детали, изготовленной из латуни, объемом $0,15 м^3$.

Из таблицы 1 предыдущего параграфа берем значение плотности латуни. Она равна $8500 \frac{кг}{м^3}$.

Дано: $\rho = 8500 \frac{кг}{м^3}$ $V = 0,15 м^3$

Найти: $m -?$

Показать решение и ответ

Скрыть

Решение: $m = \rho \cdot V$ $m = 8500 \frac{кг}{м^3} \cdot 0,15 м^3 = 1275 кг \approx 1,3 т$

Ответ: $m = 1275 кг \approx 1,3 т$.

Зачем и кому нужно знать эти формулы

В любой стране есть стандарты, по которым производится продукция. Неважно, какая это отрасль – пищевая, химическая или другая. Стандарты также могут быть мировыми. Так вот для того чтобы выпускаемая на заводах продукция соответствовала этим стандартам и нужны знания о плотности, массе и объёме.

Но зачем кому-то придерживаться чьих-то правил? Для начала, эти правила взяты не с потолка. К этому пришли разные бизнесмены со всего мира и нашли оптимальное решение, удовлетворяющее как производителей, так и конечных пользователей продукта. Если бы все выпускали продукцию как им вздумается, то людям было бы очень тяжело выбрать производителя. Ведь даже сейчас, со всеми стандартами и ГОСТами выбор просто огромный.

Кроме того, игнорируя физику и математику, можно выработать продукцию себе же в убыток или сделать продукцию, которая не оправдает ожиданий и будет выглядеть не так, как задумывал производитель. Есть и другие ситуации, где необходимы знания подобного рода – при подсчёте планируемого объёма, который займёт продукция на складе; вес продукции, которую нужно будет перевести и т.д.

Эти знания могут потребоваться инженерам, технологам, конструкторам и прочим профессиям, чья деятельность связана с физическими материалами. Конечно, для простого обывателя эти знания могут и не пригодиться. Однако, стоит вспомнить про случай с Архимедом и тогда вы поймёте, что знания – защита от обмана и настоящая сила!

Расчет объема тела по его плотности

Подобным образом выразим из формулы плотности объем:

$$V = \frac{m}{\rho}$$

Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.

Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.

Рассмотрим пример задачи на расчет объема. Молоко в бутылке имеет массу 1,03 кг. Рассчитайте объем бутылки.

В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 \frac{кг}{м^3}$.

Дано: $\rho = 1030 \frac{кг}{м^3}$ $m = 1,03 кг$

Найти: $V -?$

Решение: $V = \frac{m}{\rho}$ $V = \frac{1,03 кг}{1030 \frac{кг}{м^3}} = 0,001 м^3 = 1 л$

Ответ: $V = 0,001 м^3 = 1 л$.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Как найти массу растворенного вещества формула?

Массу растворённого вещества вычислим по формуле: m ( в − ва ) = w ( в − ва ) ⋅ m ( р − ра ) ; m ( H 2 SO 4 ) = w ( H 2 SO 4 ) ⋅ m ( р − ра ) = 0,64 ⋅ 200 = 128 г.

Интересные материалы:

Сколько заряжается Ми Бэнд 4? Сколько заряжать i12 Tws? Сколько зарплата у мичмана? Сколько зарплата у оперативника? Сколько ждать пособие на ребенка? Сколько ждать выписку из ЕГРН через МФЦ? Сколько живут пельмени? Сколько живут вороны долгожители? Сколько жизней унесла Первая мировая война? Сколько зон у корня?

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

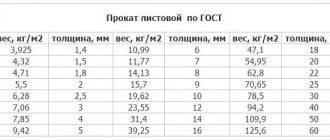
По справочникам

Сборник справочных материалов содержит таблицы металлов, по которым легко определить вес металлопроката любого вида, из черного и цветного металлов или сплавов. Кроме этого, в сборнике приведены формулы, чтобы посчитать вес металла по размерам для заготовок различных конфигураций, данные по удельному весу металлов.

К справочнику приходится обращаться при самостоятельном произведении математических расчетов, например, к таблице плотности металлов. Чтобы вычислить массу детали из цветного металла, понадобится переводной коэффициент.

С готовой таблицей легко самостоятельно рассчитать вес листа металла. По данной толщине и марке стали находится теоретический вес 1 м2, искомая величина умножается на площадь листа. Особенно это удобно для стали с рифлением, выступами, цинковым напылением, учитывается также способ прокатки (холодный или горячий).

Упрощается просчет массы швеллера и двутавра – изделий со сложным сечением. Для них есть таблица с указанием номера профиля и соответствующего веса 1 пог. м в кг. Не нужно заморачиваться, чтобы вычислить вес стальной арматуры, к тому же в таблице указано количество погонных метров в 1 т.

Аналогичные таблицы существуют для металлических профилей Г-образного сечения: указан вес 1 м уголка для конкретной толщины и ширины полки. Правда, такие расчеты отличаются от фактического веса, так как таблицы составлены на основе ГОСТа. В реальности же прокат не всегда соответствует государственным стандартам.

Плотность стали зависит от температурных показателей. Все табличные данные соответствуют температуре 20°C. Данное замечание не относится к цветному прокату.