Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!
Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.
Читать дальше!
Содержание
Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.
Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.
Сегодня мы познакомимся с такой характеристикой как плотность, она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Опытное подтверждение
Рассмотрим опыт, представленный на рисунке 1.
Рисунок 1. Взвешивание двух одинаковых тел, состоящих из разных веществ.
Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.
Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.
В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.
Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.
На рисунке изображены 3 тела массой 100 г: лед, железо и золото.
Рисунок 2. Тела одинаковой массы, но состоящие из разных веществ.
Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.
Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.
Какая плотность воды?
Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:
Стол
Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.
Столы
Определение плотности вещества
Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.
Рассмотрим два тела объемом $1 м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.
Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 м^3$) будет имеет массу 11 300 кг.
На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.
Рисунок 3. Тела равного объема, состоящие из разных веществ.
Плотность показывает, чему равна масса вещества, взятого в объеме $1 м^3$ (или $1 см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.
Дадим определение:
Плотность — это физическая величина, которая равна отношению массы тела к его объему:
$$плотность = \frac{масса}{объем}$$
или
$$\rho = \frac{m}{V}$$
где $\rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.
Что такое формула плотности?
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:
р = м / В
Где,
V – объем & m – масса объекта.
Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:
V = м / п
Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:
т = р * V
Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.
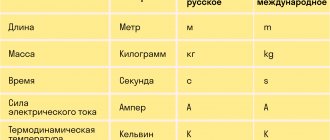
Единицы измерения плотности
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 \frac{кг}{м^3}$).
Также часто используется другая единица измерения — граммы на кубический сантиметр ($1 \frac{г}{см^3}$) (рисунок 4).
Рисунок 4. Плотности различных веществ в $\frac{г}{см^3}$.
Иногда нам потребуется переводить плотность веществ, выраженную в $\frac{кг}{м^3}$ в $ \frac{г}{см^3}$.
Давайте выразим плотность мрамора ($2700 \frac{кг}{м^3}$) в $\frac{г}{см^3}$:
$$\rho = 2700 \cdot \frac{1 кг}{1 м^3} = 2700 \cdot \frac{1000 г}{1 000 000 см^3} = \frac{2700}{1000} \cdot \frac{г}{см^3} = 2,7 \frac{г}{см^3}$$
Как найти массу через объем и плотность в физике?
Масса представляет собой количество материи, которое содержится в каком-либо теле. В свою очередь материя — это нечто, что можно физически потрогать и ощутить. Как правило, массу связывают с размерами объекта, однако это не всегда верно. Например, земной шар мог бы быть большего размера, но иметь меньшую массу. В статье рассмотрен вопрос о том, как найти массу через объем и плотность.
Понятие массы и ее появление в физике

Перед тем как рассмотреть вопрос о том, как найти массу через объем и плотность, следует понять, откуда взялась масса в физике, и что она определяет. Сам термин «масса» происходит от латинского слова massa – глыба, вещество, тело, которое, в свою очередь, берет свое начало от греческого слова μᾶζα, буквально означающего «тесто».
Масса — физическое понятие, которое указывает на количество содержащейся в теле материи. В Международной системе единиц измерения ее измеряют в килограммах. Появление в физике этого понятия связано с двумя важными законами:
- Закон всемирного тяготения.
- Второй закон Ньютона.
В соответствии с концепцией всемирного тяготения два тела притягиваются друг к другу с силой, которая пропорциональна произведению двух постоянных величин. Эти постоянные величины получили название гравитационных масс этих тел. То есть гравитационная масса тела — это свойство самой материи, благодаря которому все тела притягиваются друг к другу.
Что касается второго закона Ньютона, то следует вспомнить, что любое ускорение, вызванное действием некоторой внешней силы на данное тело, пропорционально некоторой константе, которая называется инертной массой. В этом законе инертная масса определяет меру «сложности» изменения скорости движения данного тела.
Понятие объема тела
Объем является физическим свойством материи, которое определяет занимаемое ею пространство. В Международной системе единиц он измеряется в метрах кубических, но также часто используют другие единицы измерения: кубические сантиметры и литры.
В зависимости от состояния вещества применяют различные методы измерения объема:
- Для жидких тел используют специальные градуированные прозрачные емкости (цилиндры, пробирки, пипетки и другие).
- Для твердых тел, которые сохраняют свою форму, объем измеряется исходя из их линейных размеров с применением соответствующей математической формулы. Например, параллелепипеда объем равен произведению его длины, ширины и высоты.
- Газообразные тела не сохраняют свой объем, в отличие от жидкостей и твердых тел, поэтому он для газов всегда равен объему сосуда, в котором находится газ.
Плотность вещества
Наконец, отвечая на вопрос о том, как найти массу через объем и плотность, следует разобраться с последней характеристикой — плотностью тел. Плотность является неотъемлемой физической характеристикой материи, которая связывает массу и объем, то есть она определяет, какое количество массы вещества содержится в единице объема. В Международной системе единиц она выражается в виде килограммов на метр кубический, но часто используется и в граммах на сантиметр кубический.
Любое вещество обладает конкретным значением плотности, например, в одном литре воды содержится один килограмм массы, то есть ее плотность равна 1 кг/л или 1000 кг/м3.


Понятие плотности играет важную роль в природе. Так, вопрос плавучести тел в воде является исключительно вопросом сравнения плотности тела и воды. Тела, имеющие большую плотность, чем вода, тонут в ней, например, яйцо или камень.
Как найти массу в физике через объем и плотность?


Перейдем теперь непосредственно к решению поставленной задачи. Допустим необходимо измерить массу имеющегося алмаза. Сначала нужно измерить его объем, допустим, он равен 5000 см3. Разбираясь в том, как найти массу через объем, следует также определить плотность вещества. В данном случае можно обратиться к табличным данным и посмотреть, какая плотность характерна для алмаза. В таблице находим, что она равна 3,52 г/см3.


После того как все необходимые величины определены, следует использовать известную формулу, как найти массу через объем и плотность: m = V*ρ, где V — объем тела, ρ — плотность. Подставляя полученные значения для алмаза, получаем: m = 5000 (см3)*3,52 (г/см3) = 17600.0 г = 17,6 кг. Следует обратить внимание, что при умножении объема на плотность единицы измерения объема (см3 в примере) сокращаются и остаются только единицы измерения массы.
fb.ru
Плотности различных твердых тел
| Твердое тело | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ | Твердое тело | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ |
| Осмий | 22 600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22 400 | 22,4 | Стекло | 2500 | 2,5 |
| Платина | 21 500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19 300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11 300 | 11,3 | Кирпич | 1800 | 1,8 |
| Серебро | 10 500 | 10,5 | Сахар | 1600 | 1,6 |
| Медь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Латунь | 8500 | 8,5 | Капрон | 1100 | 1,1 |
| Сталь, железо | 7800 | 7,8 | Полиэтилен | 920 | 0,92 |
| Олово | 7300 | 7,3 | Парафин | 900 | 0,90 |
| Цинк | 7100 | 7,1 | Лед | 900 | 0,90 |
| Чугун | 7000 | 7,0 | Дуб сухой | 700 | 0,70 |
| Корунд | 4000 | 4,0 | Сосна сухая | 400 | 0,40 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Таблица 1
Как вычислить молекулярную массу вещества?
Молярная масса
в Международной системе СИ измеряется в кг/моль, хотя обычно эту величину выражают в грамм/моль. Эта величина обозначается английской буквой M, а формула
молярной массы
выглядит следующим образом: M=m/v, где m –
масса
вещества, а v – количество вещества.
Интересные материалы:
Что включает понятие валовая прибыль предприятия? Что включает в себя гуманизм? Что включает в себя мучное? Что включает в себя подготовка деловых совещаний? Что включает в себя стоимость тура? Что включает в себя сухопутные войска? Что включает в себя валовая прибыль предприятия? Что выдают после окончания военной кафедры? Что выделяет CO2? Что выше магистра?
Плотности различных жидкостей
| Жидкость | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ | Жидкость | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ |
| Ртуть | 13 600 | 13,60 | Керосин | 800 | 0,80 |
| Серная кислота | 1800 | 1,80 | Спирт | 800 | 0,80 |
| Мед | 1350 | 1,35 | Нефть | 800 | 0,80 |
| Вода морская | 1030 | 1,03 | Ацетон | 790 | 0,79 |
| Молоко цельное | 1030 | 1,03 | Эфир | 710 | 0,41 |
| Вода чистая | 1000 | 1,00 | Бензин | 710 | 0,71 |
| Масло подсолнечное | 930 | 0,93 | Жидкое олово (при $400^{\circ}$) | 6800 | 6,80 |
| Масло машинное | 900 | 0,90 | Жидкий воздух (при $-194^{\circ}$) | 860 | 0,86 |
Таблица 2
Закон Авогадро и молярный объём газов
Обратите внимание на рисунки. Почему, несмотря на разные массы газов, они занимают одинаковый объём?
В начале XIX века итальянский ученый Авогадро, проведя наблюдения над свойствами газов в различных условиях и проанализировав открытые прежде законы о газах (Бойля-Мариотта, Гей-Люссака и др.) в 1811 году сформулировал новый закон о газах. Закон Авогадро звучит следующим образом: в равных объемах различных газов при одинаковых условиях (одинаковых температуре и давлении) содержится одинаковое число молекул.
Итальянский ученый. В 1811 году им был открыт закон о газах, который впоследствии был назван его именем.
Мы уже знаем, что 1 моль любого вещества содержит молекул. Согласно закону Авогадро, можно утверждать, что одинаковое число молекул в 2 г водорода, 32 г кислорода, 28 г азота, 44 г углекислого газа занимает одинаковый объём.
Было вычислено, что при нормальных условиях объем 1 моля любого газа или смеси газов составляет примерно 22,4 л. Объем 1 моля газа при нормальных условиях (н.у.) называют молярным объемом данного газа, выраженным знаком . При измерении объема газа в литрах молярный объём составит Зависимость между количеством вещества и молярным объёмом газа можно выразить следующей формулой:
Здесь — количество вещества, — объём газа, — молярный объем.
На основе закона Авогадро и молярного объёма газов можно вычислить плотность газов при нормальных условиях и относительную плотность одного газа по отношению к другому газу. Плотность обозначается буквой её единица измерения —
Нормальные условия означают: температура 0°С, 1 атм давления 1атм — 101,3 кПа
Для вычисления плотности какого-либо газа X в нормальных условиях (н.у.), следует его молярную массу разделить на молярный объем:
Например, вычислим плотности кислорода и углекислого газа при нормальных условиях:
Плотность твёрдых и жидких веществ при н.у. вычисляется по формуле .
Для того, чтобы определить, масса какого из газов с одинаковыми объемами и при одинаковых условиях бывает тяжелее, пользуются понятием относительной плотности. Отношение плотностей различных газов при одинаковых условиях равно отношению их молярных масс. Относительная плотность обозначается буквой D и не имеет единицы измерения. Формула относительной плотности следующая:
Относительную плотность газов в большинстве случаев вычисляют по самому легкому газу — водороду и воздуху:
В таком случае, относительная плотность углекислого газа по водороду вычисляется следующим образом:
Так как средняя молярная масса воздуха, состоящего из смеси газов, примерно равна 29 г/моль, то формула его относительной плотности следующая:
Плотности различных газов
| Газ | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ | Газ | $\rho, \frac{кг}{м^3}$ | $\rho, \frac{г}{см^3}$ |
| Хлор | 3,210 | 0,00321 | Угарный газ | 1,250 | 0,00125 |
| Углекислый газ | 1,980 | 0,00198 | Природный газ | 0,800 | 0,0008 |
| Кислород | 1,430 | 0,00143 | Водяной пар (при $100^{\circ}$) | 0,590 | 0,00059 |
| Воздух (при $0^{\circ}C$ | 1,290 | 0,00129 | Гелий | 0,180 | 0,00018 |
| Азот | 1,250 | 0,00125 | Водород | 0,090 | 0,00009 |
Таблица 3
В чём разница между понятиями «масса» и «количество»
Если мы будем производить подобные расчеты, соответствующие этому заданию, для простых веществ, образованных различными элементами, то всякий раз получим одно и то же число —
Например, в 1 моле водородного газа содержится молекул, в 1 моле поваренной соли (NaCI) ионов натрия и ионов хлора
Количество частиц, содержащихся в 1 моле химических веществ ( ), называется постоянной Авогадро (Na). Постоянная Авогадро отличается от числа Авогадро тем, что измеряется определенной единицей
Количество вещества можно вычислить по следующей формуле:
Здесь — количество вещества, — масса, М — молярная масса, N — заданное количество молекул, — постоянная Авогадро. Все представленные в формуле величины нам уже известны. Кроме понятия молярной массы. Давайте выясним сущность этого понятия.