Различные измерения и показатели используются в каждой фирме, в любой организации. Выбор подходов к оценке степени достижения некоторого показателя (например, плана продаж) огромен: тут сколько людей, фирм, ситуаций, видов работ, столько и мнений. Задача этой статьи не придумывать что-либо своё, а попытаться классифицировать доминирующее большинство существующих подходов к измерению показателей. В соответствии с теорией измерений при моделировании реального явления следует прежде всего установить типы шкал, в которых измеряются или должны быть измерены те или иные переменные. Что такое шкала? Какими они бывают? Какие ограничения накладываются на числа, используемые для измерений? Как правильно пользоваться шкалами, чтобы получить достоверные первичные измерения? Какие интегральные и комплексные показатели могут быть построены на множестве измерений, выполненных в различных шкалах?
Шкалы и их классификации
Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.
Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).
Шкалирование — это:
- выбор шкалы для первичных измерений;
- перевод измерения из одной шкалы в другую.
Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается. Шкалы, как правило, объединяют в три основные группы:
- номинальные — для качественных измерений;
- порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
- количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).
Иногда все шкалы измерения делят на два класса:
- шкалы качественных признаков (порядковая шкала и шкала наименований);
- шкалы количественных признаков (количественные шкалы).
Далее мы последовательно разберём все типы шкал.
Как считать очки в десятиборье?
Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.
Типы интервалов
В психологии используются разные шкалы для изучения разных характеристик социально-психологических явлений.
Первоначально выделяли четыре типа числовых систем, которые соответственно определяли четыре уровня или шкалы измерения:
- шкала имен именная;
- шкала заказов порядковая;
- интервальная шкала — интервальная;
- масштаб отношений пропорционален.
Первые две шкалы были названы неметрическими, вторые две — метрическими. В соответствии с этим психология говорит о двух подходах к психологическим измерениям: метрическому (более строгому) и неметрическому (менее строгому).
Ряд специалистов также выделяют абсолютную шкалу и шкалу разностей.
Рассмотрим особенности каждого типа весов.
Номинальные шкалы
Номинальная шкала (nominal scale), или шкала наименований 1, сопоставляет каждый объект с определённым признаком. В результате объект либо обладает этим признаком, либо нет. Номинальная шкала состоит из названий — это самое простое и в то же время верное понимание номинальной шкалы. Пример. Красное или чёрное — это измерение в некой цветовой гамме. Многие классификации, ответы на вопросы анкеты — всё это примеры номинальных измерений. С них начинается работа создателей сбалансированной системы показателей, а закончиться она должна цифрами. Но здесь важно не переборщить и оставить номинальные измерения только там, где они предпочтительнее формальной оцифровки.
Как правильно пользоваться шкалами, чтобы получить достоверные первичные измерения? Это не такой простой вопрос, как кажется на первый взгляд.
Допустимые преобразования. В номинальной шкале допустимыми преобразованиями (см. врезку) являются все взаимно-однозначные преобразования 2. Например, red — это «красный». Никаких отношений, кроме «равно» и «неравно», здесь нет. В этой шкале числа используются лишь как метки (как, например, при сдаче белья в прачечную), то есть лишь для различения объектов.
Допустимые преобразования
Этим понятием математики строго описывают шкалы. Тип шкалы задаётся группой её допустимых преобразований. Допустимые преобразования — это такие преобразования, которые не меняют соотношения между объектами измерения и, соответственно, выводы, сделанные по результатам измерений.Например, при измерении длины переход от аршинов к метрам не меняет соотношений между длинами рассматриваемых объектов: если первый объект длиннее второго в пять раз, то это будет установлено при измерении как в аршинах, так и в метрах. Обратите внимание, что при этом численное значение длины в аршинах отличается от длины в метрах — не меняется лишь результат сравнения длин двух объектов. Аналогично денежные суммы можно сопоставлять как в рублях, так и в иностранной валюте. Особенность, связанная с изменяющимися курсами валют: результат сопоставления денежных сумм в разных валютах меняется во времени. С аршинами и метрами ситуация иная: их соотношение вечно. Вот вам и проблема курсовых разниц в экономике. О ней сейчас не место говорить, но запомните её.
Порядковые шкалы
Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними. Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов. Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен. Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы. Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:
- ранговая шкала, которая предполагает присвоение объектам рангов (ранжирование);
- балльная шкала, в которой применяются баллы.
Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.
Ранговые порядковые шкалы
Ранговые шкалы — это шкалы, где числа служат только для присвоения мест. Экспертов часто просят ранжировать (упорядочить) объекты экспертизы, то есть расположить их в порядке возрастания (или убывания) интенсивности исследуемой характеристики. Ранг — это номер объекта экспертизы в упорядоченном ряду значений характеристики у различных объектов. Формально ранги выражаются числами 1, 2, 3…. Важно помнить, что измерения 1, 2, 3 и 6, 10, 50 означают одно и то же: первая альтернатива заняла первое место, вторая — второе место и т. д. В ранговых шкалах нет информации о величине различий между оцениваемыми объектами. Такие шкалы используются тогда, когда объект трудно описать несколькими характеристиками, которые потом оцениваются качественно (баллами, например) или количественно. В практике менеджмента рейтинги часто основаны на ранговых шкалах.
Ранговые измерения (процедуры ранжирования). Различают несколько основных типов алгоритмов ранжирования:
- процедура непосредственного ранжирования, когда эксперт должен просто упорядочить объекты. При ранжировании он располагает объекты в порядке предпочтения, руководствуясь знаниями, собственными соображениями и пр. — по сути, расставляет объекты в определённом порядке, пользуясь своим собственным алгоритмом и не объсняя, почему он выбрал именно этот вариант;
- процедура опосредованного ранжирования, когда эксперт должен упорядочить объекты и дать пояснения;
- процедура последовательного непосредственного ранжирования, когда эксперт сначала должен отнести объекты к одному из нескольких классов, которым заранее присвоил ранги, а затем упорядочить объекты внутри каждого класса. Метод используется при большом количестве объектов ранжирования;
- «метод пузырька» взят из программирования, где он применятется для сортировок. Эксперт должен найти место (N+1)-ого объекта в ряду уже упорядоченных N-объектов. Такая процедура весьма экономна и точна;
- процедура парных сравнений заключается в том, что эксперт устанавливает порядок объектов путём сравнения всех возможных их пар. Это самый точный, но и самый трудоёмкий метод. Перевод результатов таких парных сравнений в ранги не так прост, пример неверного перевода результатов парных сравнений в ранги приведен во врезке.
Простейший (и неверный) перевод результатов парных сравнений в ранги и в весовые коэффициенты
Заманчива идея получить весовые коэффициенты, то есть количественную меру, из порядковых измерений. Однако, как правило, такое действие некорректно — оно многозначно и потому единственный и корректный вывод для задач менеджмента невозможен. Вместе с тем оно популярно, особенно среди людей, плохо знающих математику. Приведём пример наиболее простой и популярной модификации метода парных сравнений. Допустим, эксперт проводит оценку четырёх методов, которые связаны с решением кадровых вопросов в корпоративном проекте: Z1 — повышение квалификации в процессе выполнения проекта; Z2 — привлечение кадров со стороны; Z3 — подготовка кадров в своём корпоративном университете; Z4 — разовое повышение квалификации.
| Zi/Zj | Z1 | Z2 | Z3 | Z4 |
| Z1 | 1 | 1 | 1 | |
| Z2 | 0 | 0 | 0 | |
| Z3 | 0 | 1 | 1 | |
| Z4 | 0 | 1 | 0 |
Составим матрицу бинарных предпочтений эксперта, где 1 означает, что один метод „предпочтительнее”, чем другой, с которым он сравнивается. Определим оценку каждого метода (складываем по строкам): C1 = 3; C2 = 0; C3 = 2; C4 = 1. Получаем порядок предпочтения методов: Z1, Z3, Z4, Z2. Пока всё это корректные действия. Затем наступает черед „творчества”. Простейший (и неверный) перевод результатов парных сравнений в весовые коэффициенты. Если нужны „веса” указанных четырёх альтернатив, то можно нормировать числа {С} и получить „веса” {v} делением каждого значения С на сумму всех Сi, равную шести: v1 = 3/6 = 0,5; v2 = 0; v3 = 0,33; v4 = 0,17. Проверка: сумма весов должна быть равна 1. Однако анализ корректности метода даёт отрицательный результат. Дело в том, что объектам могут быть присвоены и другие веса (см. подобный пример ниже). Почему некорректно? Потому что в результате его применений вес v1 оказывается в три раза больше, чем v4, а этого эксперт, который проводил парное сравнение, не утверждал! Подделка очевидна, так как в результате обработки мы добавили весомую толику информации от себя к тому, что говорили эксперты.
Корректные методы перевода результатов парных сравнений в шкалу интервалов. Они существуют. Считая предпочтение некоторой случайной величиной, отражающей истинное соотношение характеристик объектов сравнения, можно решить задачу определения вероятности истинного соотношения сравниваемых объектов (модели Брэдли-Терри, Терстоуна-Мостеллера, Льюса и др.). Пример такого корректного перевода дан во врезке. Большого практического значения он не имеет, и чтобы понять его суть, надо хорошо знать математическую статистику 3. Но важно понимать, что такие методы существуют и у них есть обоснование, пусть и небесспорное. В результате метод парных сравнений позволяет определить значимость различий положения тех или иных объектов в иерархии, а также решать другие сходные задачи.
Корректный перевод результатов парных сравнений в интервальную шкалу
При опросе экспертов в августе 2001 г. попарно сравнивалось качество бензина в четырех , «Лукойл», «Юкос» и «Татнефть». При сравнениях четырёх компаний получается 6 пар для сравнения:Таблица 1. Сравнение компаний по качеству бензина
| Пары | Частота выбора первого элемента пары | Частота выбора второго элемента пары |
| «ТНК» — «Лукойл» | π(1,2) = 0,508 | π(2,1) = 0,492 |
| «ТНК» — «Юкос» | π(1,3) = 0,331 | π(3,1) = 0,669 |
| «ТНК» — «Татнефть» | π(1,4) = 0,990 | π(4,1) = 0,010 |
| «Лукойл» — «Юкос» | π(2,3) = 0,338 | π(3,2) = 0,662 |
| «Лукойл» — «Татнефть» | π(2,4) = 0,990 | π(4,2) = 0,010 |
| «Юкос» — «Татнефть» | π(3,4) = 0,997 | π(4,3) = 0,003 |
По результатам парных сравнений удалось выразить „качество бензина” V1, V2, V3, V4 в шкале интервалов (см. ниже). Легко заметить, что „ценности” V1, V2, V3, V4 измерены в шкале интервалов. Начало координат можно выбрать произвольно, поскольку вероятности результатов сравнения зависят только от попарных разностей „ценностей” V1, V2, V3, V4. Например, примем, что V4 = 0. Для оценки использовалась модель Терстоуна-Мостеллера, согласно которой погрешности мнений экспертов являются независимыми, нормально распределёнными случайными величинами с нулевым математическим ожиданием и дисперсией σ2. Поскольку дисперсия разности наших условных случайных величин V1, V2, V3, V4 равна 2σ2, единицу измерения удобно выбрать так, чтобы 2σ2 = 1. В результате получим следующие значения: V1(«ТНК») = V2(«Лукойл») = 2,326348, V3(«Юкос») = 2,747781, V4(«Татнефть») = 0. Таким образом, самый качественный бензин у «Юкоса»; несколько хуже у «ТНК» и «Лукойла», одинаковых по данному показателю, а у «Татнефти» значительно хуже тройки лидеров.
Energy education
Экспериментальное исследование систем
Часто недостающую информацию о системе можно получить только из самой системы, проведя специально спланированный для этого эксперимент. Содержащуюся в протоколе эксперимента информацию извлекают, подвергая полученные данные обработке, преобразованию в форму, пригодную для включения ее в модель системы. Завершающим действием является коррекция модели, включающая полученную информацию в модель.
Легко воспринимается, что эксперимент нужен для совершенствования модели. Важно понять также, что эксперимент невозможен без модели. Они находятся в одном цикле. Однако вращение по этому циклу напоминает не вращающееся колесо, а катящийся снежный ком — с каждым оборотом он становится все больше, весомее.
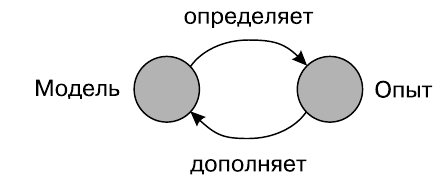
Эксперимент и модель.
Разнообразие экспериментов можно упрощенно описать их классификацией. Если мы не вмешиваемся в ход событий, а только регистрируем, что происходит на входах и выходах интересующей нас системы, то опыт называется пассивным экспериментом (или наблюдением). Если же мы не только созерцаем (и фиксируем) происходящее на входах и выходах, но и воздействуем на некоторые из них (одни намеренно поддерживая неизменными, другие — меняя должным образом), то опыт называется активным (или управляемым) экспериментом. Как и любая классификация, эта лишь приближенно описывает реальность. В абсолютно чистом виде эти два эксперимента невозможны: активный — потому, что все входы и выходы контролировать невозможно (некоторые даже неизвестны), пассивный — потому, что всякое измерение и наблюдение — взаимодействие, и вовсе не вмешаться в получаемый результат нельзя.
Ближайшими реальными, близкими к идеальным, экспериментами являются активный лабораторный опыт и пассивные наблюдения в астрономии, истории, археологии, психологии и т.п.
Еще одна важная классификация — деление экспериментов на прямые и косвенные. Прямой эксперимент — это наблюдение непосредственно той характеристики, которая нас интересует. Иногда интересующая нас характеристика не поддается прямому измерению, но есть наблюдаемая величина, связанная с нею, из наблюдений которой можно извлечь нужную нам информацию; это и будет косвенное наблюдение. Деление измерений на прямые и косвенные важно потому, что их надо обрабатывать по-разному, даже если они описаны в одинаковой шкале.
Осуществившиеся результаты эксперимента фиксируются в виде протокола наблюдений. Эта запись — не сам эксперимент, а описание его результата, т.е. его модель. Понимая термин «язык» широко, можно сказать, что протокол наблюдений — это запись результатов эксперимента на некотором языке. Разнообразие экспериментов таково, что одним языком не обойтись; существует несколько таких языков, называемых измерительными шкалами. Следует ознакомиться с ними, так как в практике придется иметь дело с обработкой данных в разных шкалах, а делать это нужно пооразному для каждой шкалы. Как в любом языке, неправильно построенная фраза теряет смысл, так и неправильно преобразованные данные эксперимента не несут ожидаемой информации.
Измерительные шкалы.
На примере измерительных шкал можно проследить явление, характерное для всех языков: начиная с универсального, но малоинформативного языка, можно, включая, присоединяя к нему дополнительную информацию, получать все более и более информативные языки, вплоть до наиболее математизированного.
1. Шкала наименований (номинальная, классификационная).
Простейшей моделью разнообразия является классификация. Она и положена в основу шкалы наименований. Измерение в этой шкале состоит в том, чтобы, произведя наблюдение классификационных признаков объекта, определить, к какому классу он относится, и записать это с помощью символа, обозначающего данный класс. Фамилии, диагноз заболевания, номера домов, автомобилей, игроков спортивных команд, названия цветов, адреса и т.д. — примеры наблюдений в номинальной шкале.
Поскольку единственным отношением, определяющим шкалу, является отношение эквивалентности (объект либо принадлежит к данному классу, либо нет), то единственной допустимой операцией над данными в этой шкале является проверка на совпадение.
Сравнивать между собой данные в номинальной шкале, полученные разными исследователями, можно, только если они пользовались одинаковым разбиением на классы (число классов и границы между ними должны совпадать). Отличаться могут лишь наименования классов и порядок их перечисления, как не нарушающие природной структуры данных.
2. Шкала порядковая (ординальная, ранговая).
Если ввести между классами номинальной шкалы дополнительное отношение порядка (предпочтения), получится новая, усиленная в информационном смысле шкала, называемая порядковой или ординальной. Примерами наблюдений, регистрируемых в порядковой шкале, являются: армейские и чиновничьи звания, школьные оценки, магнитуда землетрясений (шкала Рихтера), твердость минералов (шкала Мооса), сила ветра (шкала Бофорта), призовые места в соревнованиях. Допустимое преобразование теперь дополняется операцией проверки предпочтения. Разновидностями предпочтений являются упорядочивание при наличии стандартных опорных образцов (например, шкала Мооса основана на десяти конкретных минералах разной твердости), при нечетко заданных образцах (шкала силы ветра, школьные оценки), при отсутствии образцов (спортивные соревнования, музыкальные конкурсы). Кроме шкал совершенного порядка, однозначно определяющих предпочтения (нумерация очередности, воинские звания и т.п.), существуют шкалы квазипорядка, когда некоторые элементы упорядоченного ряда неразличимы, а также шкалы частичного порядка, когда имеются несравнимые между собой пары классов. В порядковых шкалах не существует понятия расстояния между классами, поэтому любые преобразования, сохраняющие порядок («монотонные») не влияют на информативность данных.
3. Шкала интервалов (разностей).
Если упорядочение объектов можно выполнить настолько точно, что известны расстояния между любыми двумя из них, то измерение станет заметно более информативным, чем в шкале порядка. Естественно выражать все расстояния в единицах, хотя и произвольных, но одинаковых по всей длине шкалы. Это означает, что объективно равные интервалы измеряются одинаковыми отрезками шкалы, где бы они на ней ни располагались.
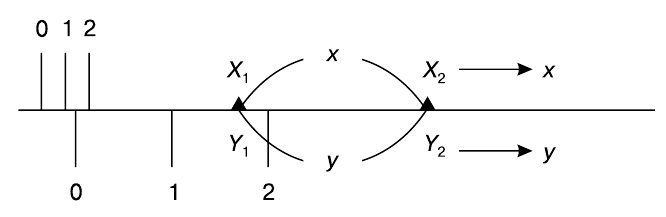

Шкала интервалов.
В итоге оказывается, что у нашей новой шкалы — шкалы интервалов — начало отсчета и единица длины интервала произвольны. Примеры наблюдений, фиксируемых в шкале интервалов: температура (шкалы Цельсия, Фаренгейта, Кельвина); летоисчисление (от Рождества Христова, от переезда Мухаммеда в Медину — на 622 года позднее, от императорской династии в Китае — на 5000 лет раньше); высота местности (от уровня моря; Голландия почти вся имеет отрицательную высоту).
Единственной новой допустимой операцией первичной обработки над данными в новой шкале является вычитание, т.е. определение интервала между двумя отсчетами. Например, если сказать, что температура увеличилась в два раза при нагреве от 9° до 18° по Цельсию, то для привыкших пользоваться шкалой Фаренгейта это будет звучать весьма странно, так как в этой шкале температура изменится от 48.2° до 64.4°. Операция деления для данной шкалы недопустима. Только интервалы имеют смысл настоящих чисел. Над ними (вторичная обработка) уже можно выполнять любые арифметические действия, а также статистические и другие процедуры.
4. Шкала циклическая (периодическая, разностей).
Есть специальный вид интервальной шкалы, который характерен тем, что она замкнута на себя, т.е. после прохождения определенного периода ее значения повторяются. Примерами являются: угловые направления из одной точки (шкала компаса, роза ветров), время суток (циферблат часов), фаза периодических колебаний (в градусах или радианах), географическая долгота (в градусах). Все сказанное об интервальной шкале относится и к циклической. Чтобы не возникло недоразумений, отметим, что сложение часов — не сложение самих временных отметок (что является недопустимой операцией), а сложение временных интервалов, т.е. вторичная обработка. Надо еще помнить об условности начала отсчета (например, при переходе на зимнее время, при пересечении линии смены дат и т.п.). Данную шкалу еще называют шкалой разностей, так как она инвариантна к сдвигу на интервал, называемый периодом шкалы.
5. Шкала отношений.
Введение еще одного определяющего отношения придает дополнительное усиление измерениям. Потребуем, чтобы не только отношения величин одного интервала в разных шкалах были константой, где бы этот интервал ни находился, что характерно для шкалы интервалов, но чтобы и отношения значений одной и той же величины, измеряемой в разных шкалах, тоже были константой, какое бы место эта величина ни занимала в реальности. Получаемая шкала именуется шкалой отношений. При этом, хотя единица измерений остается произвольной, нулевая отметка становится абсолютной, несдвигаемой. Примерами величин, природа которых соответствует шкале отношений, являются: длина (измеримая в см, футах, аршинах, км и т.д.); вес (кг, фунты, пуды, тонны и т.д.); объем (м3, баррели, литры и т.д.); деньги (рубли, доллары, евро, йены и т.д.). Данные в шкале отношений в еще большей степени становятся числами: в первичной обработке с ними имеют смысл любые арифметические операции, то же можно делать и во вторичной.
6. Абсолютная шкала.
Предыдущие «числовые» шкалы (интервальная и отношений) имели степени свободы: интервальная — две (произвольный нуль и единицу), отношений — одну (фиксированный, несдвигаемый нуль и произвольную единицу). Характерно, что «числовые» возможности данных в этих шкалах были ограничены: в интервальной шкале — операцией разности, в шкале отношений — арифметическими операциями.
Рассмотрим такую шкалу, которая имеет и абсолютный нуль, и абсолютную единицу. Эта шкала не имеет степеней свободы, она единственна, уникальна. Именно такими качествами обладает числовая ось, которую естественно назвать абсолютной шкалой. Важная отличительная особенность абсолютной шкалы состоит в том, что значения данных в ней не имеют размерности, наименований, ее единица абсолютна («штука»). Это придает данным в этой шкале особый статус (в английском языке их называют pure numbers — чистые числа) — с ними можно производить такие операции, которые недопустимы с поименованными числами. Их можно употреблять в качестве показателя степени, основания логарифма, над ними допустимы любые тригонометрические и другие трансцендентные преобразования.
Обсужденные выше шесть измерительных шкал не исчерпывают многообразия языков, на которых можно говорить о разнообразии реальности. Но они являются базовыми: остальные шкалы — производные от них, учитывающие некие сторонние, побочные, специфические условия.
До сих пор речь шла о шкалах, основанных на четкой классификации: элемент либо принадлежал к классу, либо нет. Реальная жизнь привела к необходимости рассмотрения случаев, когда требование жесткой эквивалентности не выполняется, т.е. когда элемент может одновременно принадлежать к двум и более классам. Для описания таких ситуаций разработаны два подхода.
Первый основан на теории расплывчатых (нечетких) множеств. В этой теории принадлежность к классу описывается функцией принадлежности, которая характеризует степень уверенности, с которой мы относим объект к классу. Например, в какой степени сорокалетний человек относится к классу «молодые люди», а в какой степени к «немолодым»? В этой теории измерительной шкалой является шкала значений функции принадлежности.
Второй подход состоит в учете того, что распределения вероятностей классифицируемых переменных могут перекрываться. Принимая решение о принадлежности величины к тому или другому классу, мы рассекаем область значений переменной на четкие классы, в результате чего появляются вероятности ошибок. Обработкой случайных переменных занимается развитая область знаний — математическая статистика.
При осуществлении эксперимента получаемый информационный «урожай» зависит от ряда факторов:
- как был организован опыт, какие значения и в каком порядке придавались управляемым переменным;
- каковы шумы, погрешности, искажения наблюдаемых переменных;
- насколько справедливы предположения, заложенные в нашу модель исследуемой системы;
- каковы способы, алгоритмы обработки полученных экспериментальных данных.
Значимость этих факторов различна в разных опытах, поэтому развиты специальные теории о том, как повысить качество выводов в зависимости от конкретной комбинации факторов. Практика показывает, что специалисты часто, пытаясь облегчить себе задачу, пренебрегают некоторыми тонкостями анализа данных, искренне полагая, что они несущественны. Типичным примером является нередко применяемая «оцифровка» качественных данных — классам в порядковой и номинальной шкалах присваиваются номера, а дальше эти номера обрабатываются не как символы, а как числа, с помощью арифметических операций. Но ведь это недопустимые операции для этих шкал! Другой пример — ослабление данных для приведения их к однообразию. В таблице с разношкальными данными сильные шкалы огрубляются до самой слабой (обычно порядковой), так что протокол эксперимента становится одношкальным, что облегчает обработку. В отличие от оцифровки, здесь происходит не навязывание чуждой информации, а отказ от части полезной. Это тоже снижает качество выводов.
Главной задачей при изложении данного этапа является направить внимание пользователя услуг по проведению экспериментов на проверку того, а не случилось ли использования недопустимых операций при обработке данных. Например, все числовые шкалы оперируют цифрами. Но мы уже знаем, что цифры в шкале интервалов, отношений и абсолютной должны обрабатываться по-разному. При приемке заказа рекомендуется посмотреть, нет ли в алгоритме обработки недопустимых операций.
Еще один важный момент следует иметь в виду — речь идет о согласовании информационной силы измерительной шкалы с информационным потенциалом наблюдаемого явления. Чем сильнее шкала, тем больше «информационный урожай» с эксперимента. Поэтому каждый экспериментатор старается использовать как можно более сильную шкалу. Но ведь нельзя наблюдение с произвольно устанавливаемым нулем считать принадлежащим к шкале отношений. Таким образом, при прямых наблюдениях желательно шкалу измерений делать посильнее, но не сильнее самой природы явления.
Дело еще более осложняется при косвенных наблюдениях. Наблюдаемая величина, косвенно связанная с интересующим нас ненаблюдаемым явлением, может принадлежать к любой, в том числе и к самой сильной шкале; тогда как информационный потенциал самого явления может быть существенно ниже. Как обрабатывать данные эксперимента? Ответ состоит в том, чтобы при обработке косвенных данных, в сколь бы сильной шкале они ни фиксировались, не употреблять операций, недопустимых в шкале, отвечающей природе исследуемого явления.
Балльные порядковые шкалы
Балльные шкалы используются очень часто, примеры мы уже приводили. Однако важно понимать, что каждому баллу необходимо присвоить качественную характеристику, в противном случае может пострадать корректность. Приведу пример: в конце 1990-х гг. я был назначен ответственным преподавателем (качество, контроль, апелляции) на устном экзамене по экономике для абитуриентов НИУ ВШЭ. Только что на ректорате ввели 10-балльную шкалу. Экспромт не удался — первый блин, как обычно, вышел комом. Моя работа заключалась, в том числе, и в „обеспечении справедливости”, то есть чтобы за примерно одни и те же ответы преподаватели в разных комиссиях ставили одинаковые баллы. Разброс в оценках оказался ужасающим — от 4 до 7 за похожие ответы. Буквально на следующий день ошибка в дефиниции шкалы была исправлена, а получившаяся шкала (см. таблица 2) успешно работает до сих пор (с небольшим изменением). Многие вузы взяли её на вооружение. Обращаю внимание читателей, что в соответствии со спецификой каждого предмета преподаватель конкретизирует шкалу.
Таблица 2. Пример 10-балльной шкалы для оценки успеваемости студентов.
| Балл | Качественная характеристика |
| 10 | Пять с плюсом — исключительные знания (кое-что из ответа студента даже преподаватель не знал) |
| 9 | Отлично, твёрдая пятёрка |
| 8 | Пять с минусом |
| 7 | Четыре с плюсом |
| 6 | Четыре, твёрдая четвёрка |
| 5 | Четыре с минусом |
| 4 | Три с плюсом |
| 3 | Три, твёрдая оценка «удовлетворительно» |
| 2 | Три с минусом |
| 1 | Неудовлетворительно |
Важный вопрос: какова идеальная размерность балльной шкалы? Ответ: сколько качеств, столько и баллов. Баллы обозначают упорядоченные качества, и каждому качеству присваивают свой балл. Обратное неверно: если взять за основу 10-балльную шкалу и каждому баллу попытаться „присвоить” определённое качество, то можно столкнуться с ситуацией, что качеств может оказаться не 10, а всего 7. Поэтому следует отталкиваться именно от количества качеств, которые вы можете выделить.
Если нет обоснования логики присвоения баллов, будем считать измерение некорректным. Это необходимо для корректного выставления балльных оценок.
Балльные измерения. Балльные измерения формально просты, но коварны возможностью допустить необоснованные оценки и тем самым всё испортить. Существует два подхода к выставлению балльных оценок:
- непосредственная балльная оценка представляет собой приписывание объектам баллов на основании субъективного представления. Такая оценка используется в социологии, но в управлении компанией применяться не должна (за исключением, пожалуй, начальной стадии разработки системы показателей). Причина проста — слишком произвольно баллы приписываются объектам, трудно объяснить, почему мы по 10-балльной шкале ставим 5, а не 6, например;
- балльная оценка с обоснованием — это процедура приписывания объектам баллов на основании степени близости к описанным баллами качествам. На мой взгляд, это необходимо для корректного выставления балльных оценок. Примем следующее правило если нет обоснования логики присвоения баллов, будем считать измерение некорректным.
Перевод результатов балльных оценок в весовые коэффициенты. Если такой перевод делается одним экспертом — это операция сомнительная, но популярная. Во врезке приведён один из популярных методов — метод последовательных сравнений.
Перевод рангов в весовые коэффициенты одним экспертом. Метод последовательных сравнений
Продолжим пример, приведённый во врезке. Итак, эксперт проводит оценку четырёх целей, связанных с решением кадровой проблемы. Варианты ранжируются таким образом: Z1, Z3, Z4, Z2. Шаг 1. Все оцениваемые объекты располагаются в порядке убывания их важности. Назначаются предварительные оценки важности, сумма которых отличается от 100. При этом первый объект массива получает оценку 100, остальные — в соответствии с их важностью. Выставляем предварительные оценки (условные баллы): p1 = 100, p3 = 60, p4 = 40, p2 = 10. Шаг 2. Первый объект массива сравнивается со всеми возможными комбинациями нижестоящих объектов, причём в каждой комбинации берётся по два таких объекта. Считается, что комбинацию можно рассматривать как сумму, то есть оба объекта „реализуются”. При необходимости оценка первого объекта корректируется. Выполним сравнение целей и корректировку их оценок: Z1 сравниваем с (Z3 и Z4) (то есть цель Z1 сравниваем с комбинацией Z3 и Z4), затем Z1 сравниваем с (Z3 и Z2) и так далее. Допустим, эксперт полагает, что Z1 лучше, чем Z3 и Z4 вместе взятые, но Z3+Z4 в сумме составляют 100 условных баллов, поэтому корректируем оценку: p1 = 125. Шаг 3. Второй объект массива сравнивается со всеми возможными комбинациями нижестоящих объектов, причём в каждой комбинации снова берётся только по два таких объекта. При необходимости корректируется оценка второго объекта и т. д. Например, Z3 сравниваем с (Z4 и Z2). Остальные сравнения не приносят ничего нового. Шаг 4. Производятся нормирование скорректированных оценок и расчёт на их основе весов объектов. Запишем скорректированные оценки и вычислим веса целей: p1 = 125; p3 = 60; p4 = 40; p2 = 10; v1 = 125/сумма всех оценок = 0,54; v3 = 0,25; v4 = 0,17; v2 = 0,04. Теперь эти веса можно использовать в аддитивной функции полезности 4. Корректность вычислений вам предстоит оценить позже, после знакомства с количественными шкалами и оценками, получаемыми на основе измерений в них.
Количественные шкалы
Количественные шкалы отражают более высокий уровень измерений, учитывающий не только то, в каком отношении измеряемый объект находится с другими объектами, но и степень их различия. Примеры использования количественных шкал мы видим повсюду. Допустимые преобразования. Количественные шкалы определены с точностью до преобразований, которые не меняют единицы измерения (линейных или иных функциональных преобразований). Типы количественных шкал. Различают количественные шкалы:
- интервалов;
- степеней;
- отношений;
- разностей;
- абсолютную шкалу.
Расположение шкал в этом списке не случайно. Первая (шкала интервалов) — самая слабая по информативности и самая сильная в плане надёжности оценок, последняя (абсолютная шкала) — наиболее информативная (измерения могут быть очень надёжными), но при этом допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу максимально затруднена — помните разницу между оценкой и измерением? Шкала интервалов (интервальная шкала) точно определяет величину интервала между точками на шкале. Для проведения измерений необходимо задать интервал (2 точки). Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования вида: F(Х) = а · Х + b, где а > 0.
Шкала степенная. Шкала степеней (степенная) допускает степенное преобразование (F(Х) = АХВ). В области техники она вполне адекватна — у неё тоже две степени свободы, как у шкалы интервалов. В экономике она, напротив, является исключением, поэтому подробно рассматривать её не будем.
Шкала интервалов — самая слабая по информативности и дающая самые надёжные оценоки. Абсолютная шкала — наиболее информативная, но допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу в абсолютной шкале максимально затруднена — помните разницу между оценкой и измерением?
Шкала отношений. Из количественных шкал в науке и практике наиболее распространены шкалы отношений. В них есть естественное начало отсчёта — ноль (то есть отсутствие величины), но нет естественной единицы измерения. Примеры использования шкалы отношений:
- измерение большинства физических единиц: массы тела, длины, а также цены в экономике;
- любое процентное соотношение — это измерение в шкале отношений;
- простые индексы типа Выручка текущего года/Выручка прошлого года также представляют собой измерение в шкале отношений.
Шкала отношений допускает преобразования, изменяющие только масштаб, то есть преобразования подобия: F(Х) = аХ, где а > 0 (линейные возрастающие преобразования без свободного члена). Примеры преобразования шкалы отношений:
- пересчёт цен из одной валюты в другую по фиксированному курсу;
- перевод массы из килограмм в фунты.
Базовая точка в шкале отношений одна — «единица». Эта условная «единица» может быть, например, 100 (проценты) или 1 (доли). Таким образом, измерения в долях и процентах эквивалентны, что очевидно и без всякой теории. Однако выводы, которые делаются по результатам процентных измерений, могут быть ошибочными (см. врезку). Возникают сопутствующие вопросы:
- встречаются ли в практике управления подобные сравнения?
- какие проценты можно сравнивать друг с другом и для чего?
- какие действия с процентами можно производить?
- какие действия можно производить с индексами?
Корректность процентных измерений. Рейтинг Путина vs стоимость свинины
- Рейтинг Путина: в январе 2014 — 60,6%, в июне 2014 — 87,4%.
- Цена свинины: в январе — 116 руб/кг, в июне — 195 руб/кг.
Вывод: по темпам роста (в научной терминологии «прироста») свинина побеждает Путина: 44% vs 68%. Корректны ли эти измерения? Решите сами и объясните (что гораздо сложнее). Точно сформулировать, насколько такие сравнения корректны, удается лишь 10% слушателей программ МВА. Это ещё один довод в пользу изучения шкал. Хотя бы на уровне знакомства.
Шкала разностей допускает преобразование сдвига: F(Х) = Х + в. В такой шкале есть естественная единица измерения, но нет естественного начала отсчета. Базовая точка в шкале разностей тоже одна — условный „ноль”, своеобразная точка отсчёта. Пример: по шкале разностей измеряется время, если естественной единицей измерения принимаем год (или сутки — от полудня до полудня). На современном уровне знаний естественное начало отсчёта указать нельзя. Даже дату сотворения мира различные авторы рассчитывают по-разному, как и дату рождения Иисуса Христа. Абсолютная шкала — это шкала, которая запрещает преобразования 5. Только для абсолютной шкалы результаты измерений (числа) используются в привычном смысле именно как числовые значения. В качестве примера измерений по абсолютной шкале можно привести число работников компании или выручку. При этом оценка выручки может отличаться от самой выручки (допустим, 20 млн руб. — „хорошо”, 24,5 млн руб. — „отлично”). Кроме перечисленных шести основных типов количественных шкал, иногда используют и иные шкалы.
Степени свободы шкал
Для проведения измерений в шкалах отношений и разностей мы должны задавать одну точку. В шкале отношений она „играет роль единицы”, то есть соответствует переводу базового эмпирического элемента в единицу действительной оси. Для шкалы разностей это „нулевая точка”, то есть нужно задать отношение таким образом, чтобы „точка отсчёта” эмпирической системы превращалась в числовой ноль. В этой связи математики различают шкалы по степеням свободы:
- 2 степени свободы имеют шкалы интервалов, степеней;
- 1 степень — шкалы отношений и разностей;
- 0 степеней — абсолютная шкала.
Понятие шкалы интервалов
Такая шкала открывает возможность определения не только отличительных характеристик предметов, но и их количества в проявлении того или иного свойства предмета. Он группирует объекты на основе большего или меньшего размера для определенного количества единиц. С существующими измерениями разрешены различные арифметические операции.
Каждый интервал характеризуется определенным размером. Размер интервала постоянен и не может быть изменен в любом месте шкалы. Для определения размеров интервала задаются единицы измерения. Для этого объекту или качеству присваивается число, которое отражает количество единиц измерения, равное размеру доступного качества.
На шкале интервалов нет точки отсчета, т.е. отсутствует нулевая отметка, указывающая на отсутствие измеряемого признака. Точнее, на шкале ноль, но это условный показатель.
Назначение шкалы интервалов — провести сравнительную характеристику двух объектов или процессов с определением преобладания определенного признака или качества в одном из них.
Анализ различных процессов и явлений с использованием интервальной шкалы позволяет использовать любые статистические методы. Вы можете использовать методы дисперсии, методы определения среднего арифметического, чтобы охарактеризовать приоритетную тенденцию развития.
Существует два основных типа интервальных шкал:
- Единые шкалы на основе выбранных единиц измерения.
- Неправильные шкалы, основанные на стандартных фундаментальных точках.
Шкала интервалов:
- Выявляет величину различия в проявлении признаков и качеств рассматриваемых предметов;
- Позволяет проводить сравнительный анализ, определяя отклонения в большую или меньшую сторону, т.е. на сколько;
- Наделен единицей шкалы.
Применение шкалы актуально для определения уровней проявления различных свойств психического и физиологического характера, определения и сравнения температурных показателей, ведения оценочной статистики в системе образования, оценки спортивных событий, результатов спортивных игр, учебных и спортивных. достижения.