Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.
Что такое класс точности прибора?
Класс точности – это характеристика прибора, которая определяется границами допускаемых основной и дополнительной погрешностей, а также другими свойствами, предусмотренными стандартами на данный вид изделия, которые оказывают влияние на точность. Этот параметр присутствует в технических характеристиках многих приборов, которые имеют эталонные выходные параметры, будь то электронные или механические измерительные устройства. Класс точности является основной характеристикой измерительной техники: весов, мультиметров, осциллографов, КИПовского оборудования и прочего. Чем выше это значение у прибора, тем больше стоит такое устройство, это связано со сложностью производства таких изделий.

Нормированная погрешность
Виды маркирования
Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.
Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.
Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.
Виды измерений


Погрешность измерения – это величина отклонения от истинного значения измеряемых показателей и величин. Для расчета используются следующие формулы:
- Абсолютная погрешность: Δ = Xд – Xизм. Рассчитывается путем вычитания от действительного числа измеренное. Выражается в единицах измеряемых показателей.
- Относительная погрешность: δ = (Δ ⁄ Xд)*100. Показывает процент отклонения по модулю и рассчитывается отношением абсолютной к действительной, умноженной на 100%.
- Приведённая погрешность: γ = (Δ ⁄ Xн)*100. Рассчитывается на основании нормирующего значения, что позволяет указать диапазон измерений. В этом случае абсолютная делится на нормирующую величину, умноженной на 100%.
Если существует комплекс приборов, то определяется совокупная характеристика. Сначала приводятся погрешности к единому виду, после чего складываются.
Пределы
Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Читайте также: Что будет, если вовремя не снять швы?
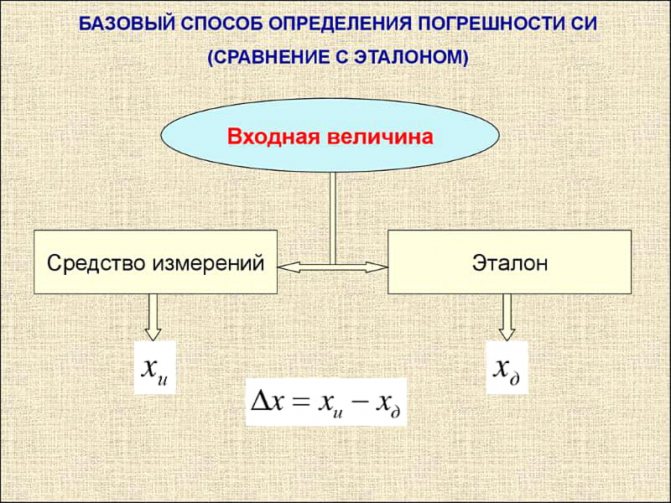
Базовый способ определения погрешности
При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.
Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.


Класс точности 2,5
Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.
Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.
Вопрос выбора
Для установки электросчётчика в частном доме или квартире подойдут модели, которые имеют класс не менее 2.
Кроме этого, отправляясь за электрическим счётчиком в магазин, следует точно знать следующие характеристики:
- Фазность электрической сети. Если электрическая сеть, которая подведена к счётчику, является однофазной, то устройство должно быть также для однофазной сети. Трёхфазный электросчётчик также можно установить для подсчёта использования электроэнергии, но такие устройства, как правило, имеют более высокую стоимость. Когда счётчик устанавливается для измерения трёхфазного тока, то на нём обязательно указывается соответствующая надпись. Для подсчёта трёхфазного тока однофазные приборы не используются.
- Нагрузка, при которой будет эксплуатироваться данное устройство. В зависимости от максимальной нагрузки, которая будет подключена к устройству подсчёта электроэнергии, выбирается модель, на корпусе которой обозначается такой показатель. Для стандартной нагрузки, которая используется в частном доме, применяются модели электросчётчиков рассчитанных на максимальный ток – 60 А. Если планируется подключать мощные отопительные электрические котлы, то электросчётчик выбирается с показателем не менее – 100 А.
- Если поставщик электроэнергии может продавать электроэнергию по 2 тарифам, то тарифность счётчика также учитывается при покупке. Значительно экономить на оплате электричества позволяет двухтарифные устройства. При использовании электроэнергии в ночное время такой счётчик будет регистрировать расход отдельно. Если поставщик электроэнергии позволяет производить такую оплату, то установка многотарифного счётчика позволит использовать электричество более рационально.
- Способ крепления. Позволяет установить прибор в уже имеющийся короб, или на место прибора который был установлен ранее.
Классификация счетчика по фазности
В зависимости от того, какой тип электросети проведен в доме (с однофазным напряжением или трехфазным), необходимо приобретать соответствующий счетчик:
- Однофазный прибор учета — устанавливается в однофазную (двухпроводную) сеть с напряжением 220 В. Такие электросети в основном проведены в квартирах, индивидуальных жилых домах, небольших магазинах, офисах.
- Трехфазный прибор учета — устанавливается в трехфазную сеть с напряжением от 380 В. Такие электросети проводятся в больших коттеджах, на промышленных объектах, в крупных магазинах, ресторанах, административных зданиях и складах, одним словом — на крупных объектах.
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Измеренная прибором величина всегда отличается от истинного значения на некоторое число, называемое погрешностью прибора. Погрешности измерительных приборов определяют поверкой, т. е. сравнением показаний поверяемого прибора с показаниями более точного, образцового прибора при измерении ими одной и той же величины. Значение измеряемой величины, определенное по образцовому прибору, принято считать действительным. Однако действительное значение отличается от истинного на погрешность, присущую данному образцовому прибору. Различают абсолютную, относительную и приведенную погрешности измерения.
Природа погрешностей и обозначения класса точности


Природа погрешностей связывается с множеством ограничений, которые пока не может преодолеть человек. Последнее связывается с используемыми материалами, с различными силами, которые воздействуют на элемент измерения. Именно поэтому в метрологии и приборостроении было решено ввести понятие класса точности прибора. Для нормирования используется несколько подходов:
- нормирование по результатам измерения;
- нормирование по верхнему пределу шкалы.
Для измерительных приборов стрелочного типа класс точности указывается в виде числа. Это число показывает максимально возможный процент отклонения. К примеру, для вольтметра, который работает в диапазоне 0-30 В при классе точности 1,0 погрешность будет составлять не более 0,3 В. В ряде случаев КТ указывается цифрой с буквой s. В этом случае берется половина деления от минимальной цены деления. Достаточно часто такой характеристикой обозначают элементы, которые не обладают шкалой, к примеру, трансформаторы тока.
Также характеристика иногда указывается арабскими или римскими цифрами, латинскими буквами. В последнем случае рассчитывается абсолютная погрешность. Для арабских цифр показатель рассчитывается на основании приведенной погрешности. В случае с римскими цифрами – по относительной погрешности.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.
Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности – 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
Относительная погрешность одного деления:
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Нормирование
Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й
Нормирование осуществляется по:
- абсолютной;
- относительной;
- приведенной.
Формулы расчета абсолютной погрешности по ГОСТ 8.401
Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.
Скачать ГОСТ 8.401-80
Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.
Регламентирующие документы


Существует несколько нормативно-технических документов, которые регламентируют понятие класса точности и погрешности. Первым документом является ГОСТ 13600-68, где установлен общие положения по делению средств измерения, а также возможные варианты нормирования метрологических показателей. Стандарт не регулирует технические моменты для каждого отдельного прибора, к ним должны применяться инструкции.
Вопросы КТ также представлены в ГОСТ 8.401-80 «Классы точности СИ общие требования». Это основной документ для метрологической службы, которая выполняет поверку приборов измерения. Документ подводит к единообразию характеристик средств измерения, что позволяет сопоставлять величины и определять комплексную погрешность систем измерений.
Источник
Для чего используются
Разнообразные виды измерительных трансформаторов встречаются как в небольших приборах размером со спичечный коробок, так и в крупных энергетических установках. Их основное назначение – понижать первичные токи и напряжения до значений, необходимых для измерительных устройств, защитных реле и автоматики. Применение понижающих катушек обеспечивает защиту цепи низшего и высшего ранга, поскольку они разделены между собой.
Понижающие средства разделяют по признакам эксплуатации и предназначены для:
- измерений. Они передают вторичный ток на приборы;
- защиты токовых цепей;
- применения в лабораториях. Такие понижающие средства имеют высокую классность точности;
- повторного конвертирования, они относятся к промежуточным инструментам.


Измерение
Измерительный трансформатор необходим для понижения высокого тока основного напряжения и передачу его на измерительные устройства. Для подключения стандартных приборов к высоковольтной сети потребовались бы громоздкие установки. Реализовывать инструменты таких размеров экономически не выгодно и не целесообразно.
Использование понижающих трансформаторов позволяет применять обычные устройства измерения в обычном режиме, что расширяет спектр их применения. Благодаря снижению напряжения, они не требуют дополнительных модификаций. Трансформатор отделяет высоковольтное напряжение сети от питающего напряжения приборов, обеспечивая безопасность из использования. От их классности зависит точность учета электрической энергии.
Защита
Кроме питания измерительных приборов понижающие трансформаторы подают напряжение на системы защиты и автоматической блокировки. Поскольку в сетевой электросети происходят перепады и скачки напряжения, которое губительно для высокоточного оборудования цепи.


В энергетических установках оборудование делится на силовое и вторичное, которое контролирует процессы первичной схемы подключения устройств. Высоковольтная аппаратура располагается на открытых площадках или устройствах. Вторичное оборудование находится на релейных планках внутри распределительных шкафов.
Промежуточным элементом передачи информации между силовыми агрегатами и средствами измерения, управления, контроля и защиты являются понижающие или измерительные трансформаторы. Они разделяют первичную и вторичную цепь от пагубного воздействия силовых агрегатов на чувствительные измерительные приборы, а также защищают обслуживающий персонал от повреждений.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.


Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Как определить класс точности манометра
Манометр — измерительный прибор, который позволяет установить значение избыточного давления, действующего в трубопроводе или в рабочих частях различных видов оборудования.
Такие приборы широко применяются в системах отопления, водоснабжения, газоснабжения, других инженерных сетях коммунального и промышленного назначения. В зависимости от условий эксплуатации измерителя существуют определенные ограничения по допустимому пределу его погрешности. Поэтому важно знать, как определить класс точности манометра.
Поверка приборов, для чего она нужна
Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.
Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.


Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.
Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.
Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже


Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Приборы, способные выполнять множество различных замеров, могут быть одновременно более двух классов.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.
- 0,1, 0,2 – считается самым высоким классом
- 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
- 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков
Примечание. На корпусе высокоточных измерителей, класс может не наносится. Обозначение таких устройств как правило выполняется особыми знаками.
Метрологические характеристики средств измерений
Обозначение классов точности
Классы точности средств измерений
Понятие о точности измерений и средств измерений
Точность результата измерений– одна из характеристик качества измерений, отражающая близость к нулю погрешности результата измерений. т.е. близость результата измерений к истинному значению величины. Но если погрешность измерений можно количественно выразить в единицах измеряемой величины или в отношении погрешности к результату измерений, то точность измерений количественно непосредственно из результата измерений определить нельзя. Поэтому обычно говорят о высокой (средней, низкой) точности измерений в качественном отношении, ориентируясь на полученную при измерениях соответственно незначительную погрешность (среднюю, высокую).
Значение точности ε иногда определяют величиной, обратной модулю относительной погрешности:
ε = 1/ | δ |, (6.1)
где δ – относительная погрешность.
Если бы точность характеризовалась значением, обратным абсолютной погрешности, то имела бы соответствующую обратную погрешности единицу измерения, что неудобно в применении. Вот почему удобнее количественно оценивать точность измерений с помощью относительной погрешности измерений.
Точность средства измерений– характеристика качества средства измерений, отражающая близость его погрешности к нулю. Считается, что чем меньше погрешность, тем точнее средство измерений.
При многократных измерениях их точность на практике определяют следующими характеристиками:
1) равноточные измерения: сходимость результатов измерений – близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью;
2) неравноточные измерения: воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).
Класс точности средств измерений– обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Это важно при выборе средств измерений в зависимости от заданной точности измерений.
Для установления классов точности средств измерений во многих странах применяются общие правила, в соответствии с которыми производится количественная оценка гарантированных границ погрешности средств измерений данного типа. В нашей стране такие правила содержатся в ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования». Класс точности не устанавливается на средства измерений, у которых отдельно нормируются систематическая и случайная составляющие основной погрешности, и в тех случаях, когда динамические погрешности являются превалирующими. Кроме того, классы точности не устанавливаются на средства измерений, при использовании которых поправки в результаты измерений с целью исключения дополнительных погрешностей вносить не предусматривается.
Классы точности указываются в частных стандартах (технических условиях), содержащих конкретные технические требования к тем или иным типам средств измерений. Если средство измерения предназначено для измерений нескольких величин (например, для измерения электрических напряжения и сопротивления), то класс точности определяется для каждой из величин. Так же определяется класс точности для средств измерений, имеющих несколько диапазонов измерений: каждый диапазон имеет свой класс точности.
Присваиваются классы точности средствам измерений при их разработке (по результатам приемочных испытаний). В связи с тем, что в процессе эксплуатации средств измерений их метрологические характеристики обычно ухудшаются, то допускается понижать класс точности по результатам поверки (калибровки) средства измерения.


Класс точности измерительных приборов в большинстве случаев выражается пределами допускаемой основной приведенной или относительной погрешности. При этом основной для определения формы представления класса точности прибора является характер изменения основной абсолютной погрешности средства измерений:
1) если основная абсолютная погрешность имеет аддитивный характер (Δ = а),то класс точности представляется пределами допускаемой приведенной погрешности γ, %:
γ = ± (Δ / ХN) · 100 % = ± р, (6.2)
где р – отвлеченное положительное число;
ХN – нормирующее значение, выраженное в тех же единицах, что и Δ;
2) если основная абсолютная погрешность имеет мультипликативный характер (Δ = bх), то класс точности представляется пределами допускаемой относительной погрешности δ, %:
δ = ± (Δ / х) · 100 % = ± q, (6.3)
где х – показания средства измерений (без учета знака);
q – отвлеченное положительное число;
3) если основная абсолютная погрешность имеет и аддитивную, и мультипликативную составляющие (Δ = а + bх),то класс точности представляется пределами допускаемой относительной погрешности δ, %:
δ = ± [с + d(|XК / x| – 1)], % (6.4)
где ХК – больший (по модулю) из пределов измерений;
c и d – положительный числа.
В некоторых случаях класс точности представляется пределами допускаемой основной абсолютной погрешности Δ, определяемыми по формулам:
Δ = ± а (6.5)
или
Δ = ± (а + bx), (6.6)
где а и b – положительные числа, не зависящие от х.
Положительные числа p, q, c, d выбираются из ряда 1·10n; 1,5·10n; (1,6·10n); 2·10n; 2,5·10n; (3·10n); 4·10n; 5·10n; 6·10n (n = 1, 0, -1, -2 и т.д.). Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.
На практике редко случается, когда абсолютная погрешность чисто аддитивна или чисто мультипликативна. Поэтому класс точности в виде формулы (6.2) устанавливается, когда мультипликативной составляющей можно пренебречь, а в виде (6.3) – когда несущественна аддитивная составляющая.
В обоснованных случаях, если пределы допускаемой основной погрешности не могут быть приведены к формулам (6.2)…(6.6), допускается класс точности устанавливать в виде более сложных формул или в виде графика.
От формы выражения пределов допускаемой погрешности средства измерений зависит способ их определения, а также обозначение класса точности на средстве измерений и в документации. Примеры обозначений классов точности и методы определения пределов допускаемых погрешностей средств измерений приведены в таблице 6.1.
Если пределы допускаемой основной погрешности выражены в форме абсолютной погрешности средства измерения, то класс точности в документации и на средстве измерения обозначается прописными буквами латинского алфавита римскими цифрами, причем меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Подобным же образом обозначаются классы точности средств измерений, для которых пределы допускаемой основной погрешности установлены в виде формулы, таблицы, графика, не соответствующих формулам (6.2) … (6.6). Соответствие букв значению абсолютной погрешности раскрывается в технической документации на соответствующие средства измерений.
Таблица 6.1
| Форма выражения погрешности | Обозначение класса точности | Способ определения пределов допускаемой основной погрешности | Пределы допускаемой основной погрешности, % | Пояснение | |
| в документации | на средстве измерений | ||||
| Приведенная погрешность, γ | Класс точности 1,5 | 1,5 | По формуле (6.2) (нормирующее значение ХN выражено в единицах измеряемой величины) | γ = ± 1,5 | Числовое значение погрешности в единицах измерения (Δ) равно: ± 1,5 % или |
| Класс точности 0,5 | 0,5 | По формуле (6.2) (если нормирующее значение ХN принято равным длине шкалы или ее части – существенно нелинейные шкалы) | γ = ± 0,5 | ± 0,5 % от ХN соответственно | |
| Относительная погрешность, δ | Класс точности 0,5 | По формуле (6.3) | δ = ± 0,5 | Числовое значение погрешности в единицах измерения (Δ) равно: ± 0,5 % от х (измеренного значения) |
Продолжение таблицы 6.2
| Класс точности 0,02/0,01 | 0,02 / 0,01 | По формуле (6.4) | δ = ± [0,02 + +0,01(|XK /x| – – 1)] | Числовое значение погрешности в единицах измерения (Δ) равно: полученное значение δ (%) от х (измеренное значение): ± δ % от х | |
| Абсолютная погрешность, Δ | Класс точности М | М | По формулам (6.5) и (6.6) | – | – |
Обозначение класса точности обычно не наносится на малогабаритные высокоточные меры (например, эталонные разновесы) или на те средства измерений, для которых классы точности не устанавливаются. Так, для многих типов радиоизмерительных приборов (генераторы высокочастотных и низкочастотных колебаний, электронно-счетные частотомеры, осциллографы и др.) в техническом описании, паспорте, технических условиях указываются формулы, позволяющие определить систематическую, случайную или общую погрешность в соответствующем диапазоне измерений с учетом влияющих величин и др. На приборе класс точности в этих случаях не указывается (не устанавливается).
Пределы допускаемой дополнительной погрешности непосредственно не учитываются при установлении класса точности средства измерения, но в соответствии с ГОСТ 8.009-84 и ГОСТ 8.401-80 предусматривается их нормирование и указание в технической документации:
— в виде постоянного значения влияющей величины (в пределах рабочих условий средства измерения) или в виде постоянных значений по интервалам влияющей величины в рабочей области;
— путем указания отношения предела допускаемой дополнительной погрешности, соответствующего интервалу значений влияющей величины в интервале рабочих условий средства измерения, к этому интервалу;
— путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.
Пределы допускаемой дополнительной погрешности устанавливают обычно в виде дольного (кратного) значения допускаемой основной погрешности средства измерения.
Пределы допускаемых погрешностей разрешается выражать не более чем двумя значащими цифрами, причем округление погрешности при установлении пределов не должно превышать 5 %.
При использовании средств измерений принципиально важно знать степень соответствия информации об измеряемой величине, содержащейся в выходном сигнале, ее истинному значению, т.е. владеть информацией о точности средства измерений и получаемого результата измерений. С этой целью для каждого средства измерений вводятся и нормируются определенные метрологические характеристики.
Метрологические характеристики – это характеристики свойств средства измерений, оказывающие влияние на результат измерения и его погрешности.
Нормируемые метрологические характеристики средства измерений– совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений.
Действительные метрологические характеристики средства измерений– совокупность метрологических характеристик данного типа средств измерений, определяемые экспериментально.
Номенклатура метрологических характеристик, правила выбора комплексов нормируемых метрологических характеристик для средств измерений и способы их нормирования определяются стандартом ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений».
Метрологические характеристики средств измерений позволяют:
— определять результаты измерений и рассчитывать оценки характеристик инструментальной составляющей погрешности измерения в реальных условиях применения средств измерений;
— рассчитывать метрологические характеристики каналов измерительных систем, состоящих из ряда средств измерений с известными метрологическими характеристиками;
— производить оптимальный выбор средств измерений, обеспечивающих требуемое качество измерений при известных условиях их применения;
— сравнивать средства измерений различных типов с учетом условий применения.
К основным метрологическим характеристикам средств измерений можно отнести:
— функция преобразования F(X).Данная функция нормируется для измерительных преобразователей и приборов с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины. Она задается в виде формулы, таблицы или графика и используется для определения значений измеряемой величины Х в рабочих условиях применения средств измерений по известному значению информативного параметра его выходного сигнала: Х = F-1(Y), F-1 – функция, обратная функции преобразования; Y – показания средства измерений;
— значение Y однозначной или значение Yi многозначной меры. Для этих характеристик нормируются номинальные или индивидуальные значения. Они используются для устройств, применяемых в качестве мер;
— цена деления шкалы измерительного прибора или многозначной меры. Нормирование цены деления производится для показывающих приборов с равномерной шкалой, функция преобразования которых отображается на именованной шкале. При неравномерной шкале нормируется минимальная цена деления;
— характеристики цифрового кода, используемого в средствах измерений и их элементах.К ним относятся: вид выходного кода, число его разрядов, цена единицы младшего разряда. Эти характеристики нормируются для цифровых приборов.
Точностные характеристики средства измерений– совокупность метрологических характеристик средства измерений, влияющих на погрешность измерения. К точностным характеристикам относят погрешность средства измерении, нестабильность, порог чувствительности, дрейф нуля и др.
Рассмотрим одну из таких характеристик – чувствительность средства измерений.
Чувствительность средства измерений – свойство средства измерений, определяемое отношением изменения выходного сигнала этого средства к вызывающему его изменению измеряемой величины. Различают абсолютную и относительную чувствительность. Абсолютную чувствительность определяют по формуле:
S = Dl / Dx, (6.7)
относительную чувствительность – по формуле:
S0 =Dl / Dx / x, (6.8)
где D1 – изменение сигнала на выходе;
х – измеряемая величина;
Dх – изменение измеряемой величины.
Порог чувствительности средства измерений– характеристика средства измерений в виде наименьшего значения изменения физической величины, начиная с которого может осуществляться ее измерение данным средством.
Обозначение классов точности
Классы точности средств измерений
Понятие о точности измерений и средств измерений
Точность результата измерений– одна из характеристик качества измерений, отражающая близость к нулю погрешности результата измерений. т.е. близость результата измерений к истинному значению величины. Но если погрешность измерений можно количественно выразить в единицах измеряемой величины или в отношении погрешности к результату измерений, то точность измерений количественно непосредственно из результата измерений определить нельзя. Поэтому обычно говорят о высокой (средней, низкой) точности измерений в качественном отношении, ориентируясь на полученную при измерениях соответственно незначительную погрешность (среднюю, высокую).
Значение точности ε иногда определяют величиной, обратной модулю относительной погрешности:
ε = 1/ | δ |, (6.1)
где δ – относительная погрешность.
Если бы точность характеризовалась значением, обратным абсолютной погрешности, то имела бы соответствующую обратную погрешности единицу измерения, что неудобно в применении. Вот почему удобнее количественно оценивать точность измерений с помощью относительной погрешности измерений.
Точность средства измерений– характеристика качества средства измерений, отражающая близость его погрешности к нулю. Считается, что чем меньше погрешность, тем точнее средство измерений.
При многократных измерениях их точность на практике определяют следующими характеристиками:
1) равноточные измерения: сходимость результатов измерений – близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью;
2) неравноточные измерения: воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).
Класс точности средств измерений– обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Это важно при выборе средств измерений в зависимости от заданной точности измерений.
Для установления классов точности средств измерений во многих странах применяются общие правила, в соответствии с которыми производится количественная оценка гарантированных границ погрешности средств измерений данного типа. В нашей стране такие правила содержатся в ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования». Класс точности не устанавливается на средства измерений, у которых отдельно нормируются систематическая и случайная составляющие основной погрешности, и в тех случаях, когда динамические погрешности являются превалирующими. Кроме того, классы точности не устанавливаются на средства измерений, при использовании которых поправки в результаты измерений с целью исключения дополнительных погрешностей вносить не предусматривается.
Классы точности указываются в частных стандартах (технических условиях), содержащих конкретные технические требования к тем или иным типам средств измерений. Если средство измерения предназначено для измерений нескольких величин (например, для измерения электрических напряжения и сопротивления), то класс точности определяется для каждой из величин. Так же определяется класс точности для средств измерений, имеющих несколько диапазонов измерений: каждый диапазон имеет свой класс точности.
Присваиваются классы точности средствам измерений при их разработке (по результатам приемочных испытаний). В связи с тем, что в процессе эксплуатации средств измерений их метрологические характеристики обычно ухудшаются, то допускается понижать класс точности по результатам поверки (калибровки) средства измерения.
Класс точности измерительных приборов в большинстве случаев выражается пределами допускаемой основной приведенной или относительной погрешности. При этом основной для определения формы представления класса точности прибора является характер изменения основной абсолютной погрешности средства измерений:
1) если основная абсолютная погрешность имеет аддитивный характер (Δ = а),то класс точности представляется пределами допускаемой приведенной погрешности γ, %:
γ = ± (Δ / ХN) · 100 % = ± р, (6.2)
где р – отвлеченное положительное число;
ХN – нормирующее значение, выраженное в тех же единицах, что и Δ;
2) если основная абсолютная погрешность имеет мультипликативный характер (Δ = bх), то класс точности представляется пределами допускаемой относительной погрешности δ, %:
δ = ± (Δ / х) · 100 % = ± q, (6.3)
где х – показания средства измерений (без учета знака);
q – отвлеченное положительное число;
3) если основная абсолютная погрешность имеет и аддитивную, и мультипликативную составляющие (Δ = а + bх),то класс точности представляется пределами допускаемой относительной погрешности δ, %:
δ = ± [с + d(|XК / x| – 1)], % (6.4)
где ХК – больший (по модулю) из пределов измерений;
c и d – положительный числа.
В некоторых случаях класс точности представляется пределами допускаемой основной абсолютной погрешности Δ, определяемыми по формулам:
Δ = ± а (6.5)
или
Δ = ± (а + bx), (6.6)
где а и b – положительные числа, не зависящие от х.
Положительные числа p, q, c, d выбираются из ряда 1·10n; 1,5·10n; (1,6·10n); 2·10n; 2,5·10n; (3·10n); 4·10n; 5·10n; 6·10n (n = 1, 0, -1, -2 и т.д.). Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.
На практике редко случается, когда абсолютная погрешность чисто аддитивна или чисто мультипликативна. Поэтому класс точности в виде формулы (6.2) устанавливается, когда мультипликативной составляющей можно пренебречь, а в виде (6.3) – когда несущественна аддитивная составляющая.
В обоснованных случаях, если пределы допускаемой основной погрешности не могут быть приведены к формулам (6.2)…(6.6), допускается класс точности устанавливать в виде более сложных формул или в виде графика.
От формы выражения пределов допускаемой погрешности средства измерений зависит способ их определения, а также обозначение класса точности на средстве измерений и в документации. Примеры обозначений классов точности и методы определения пределов допускаемых погрешностей средств измерений приведены в таблице 6.1.
Если пределы допускаемой основной погрешности выражены в форме абсолютной погрешности средства измерения, то класс точности в документации и на средстве измерения обозначается прописными буквами латинского алфавита римскими цифрами, причем меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Подобным же образом обозначаются классы точности средств измерений, для которых пределы допускаемой основной погрешности установлены в виде формулы, таблицы, графика, не соответствующих формулам (6.2) … (6.6). Соответствие букв значению абсолютной погрешности раскрывается в технической документации на соответствующие средства измерений.
Таблица 6.1
| Форма выражения погрешности | Обозначение класса точности | Способ определения пределов допускаемой основной погрешности | Пределы допускаемой основной погрешности, % | Пояснение | |
| в документации | на средстве измерений | ||||
| Приведенная погрешность, γ | Класс точности 1,5 | 1,5 | По формуле (6.2) (нормирующее значение ХN выражено в единицах измеряемой величины) | γ = ± 1,5 | Числовое значение погрешности в единицах измерения (Δ) равно: ± 1,5 % или |
| Класс точности 0,5 | 0,5 | По формуле (6.2) (если нормирующее значение ХN принято равным длине шкалы или ее части – существенно нелинейные шкалы) | γ = ± 0,5 | ± 0,5 % от ХN соответственно | |
| Относительная погрешность, δ | Класс точности 0,5 | По формуле (6.3) | δ = ± 0,5 | Числовое значение погрешности в единицах измерения (Δ) равно: ± 0,5 % от х (измеренного значения) |
Продолжение таблицы 6.2
| Класс точности 0,02/0,01 | 0,02 / 0,01 | По формуле (6.4) | δ = ± [0,02 + +0,01(|XK /x| – – 1)] | Числовое значение погрешности в единицах измерения (Δ) равно: полученное значение δ (%) от х (измеренное значение): ± δ % от х | |
| Абсолютная погрешность, Δ | Класс точности М | М | По формулам (6.5) и (6.6) | – | – |
Обозначение класса точности обычно не наносится на малогабаритные высокоточные меры (например, эталонные разновесы) или на те средства измерений, для которых классы точности не устанавливаются. Так, для многих типов радиоизмерительных приборов (генераторы высокочастотных и низкочастотных колебаний, электронно-счетные частотомеры, осциллографы и др.) в техническом описании, паспорте, технических условиях указываются формулы, позволяющие определить систематическую, случайную или общую погрешность в соответствующем диапазоне измерений с учетом влияющих величин и др. На приборе класс точности в этих случаях не указывается (не устанавливается).
Пределы допускаемой дополнительной погрешности непосредственно не учитываются при установлении класса точности средства измерения, но в соответствии с ГОСТ 8.009-84 и ГОСТ 8.401-80 предусматривается их нормирование и указание в технической документации:
— в виде постоянного значения влияющей величины (в пределах рабочих условий средства измерения) или в виде постоянных значений по интервалам влияющей величины в рабочей области;
— путем указания отношения предела допускаемой дополнительной погрешности, соответствующего интервалу значений влияющей величины в интервале рабочих условий средства измерения, к этому интервалу;
— путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.
Пределы допускаемой дополнительной погрешности устанавливают обычно в виде дольного (кратного) значения допускаемой основной погрешности средства измерения.
Пределы допускаемых погрешностей разрешается выражать не более чем двумя значащими цифрами, причем округление погрешности при установлении пределов не должно превышать 5 %.
При использовании средств измерений принципиально важно знать степень соответствия информации об измеряемой величине, содержащейся в выходном сигнале, ее истинному значению, т.е. владеть информацией о точности средства измерений и получаемого результата измерений. С этой целью для каждого средства измерений вводятся и нормируются определенные метрологические характеристики.
Метрологические характеристики – это характеристики свойств средства измерений, оказывающие влияние на результат измерения и его погрешности.
Нормируемые метрологические характеристики средства измерений– совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений.
Действительные метрологические характеристики средства измерений– совокупность метрологических характеристик данного типа средств измерений, определяемые экспериментально.
Номенклатура метрологических характеристик, правила выбора комплексов нормируемых метрологических характеристик для средств измерений и способы их нормирования определяются стандартом ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений».
Метрологические характеристики средств измерений позволяют:
— определять результаты измерений и рассчитывать оценки характеристик инструментальной составляющей погрешности измерения в реальных условиях применения средств измерений;
— рассчитывать метрологические характеристики каналов измерительных систем, состоящих из ряда средств измерений с известными метрологическими характеристиками;
— производить оптимальный выбор средств измерений, обеспечивающих требуемое качество измерений при известных условиях их применения;
— сравнивать средства измерений различных типов с учетом условий применения.
К основным метрологическим характеристикам средств измерений можно отнести:
— функция преобразования F(X).Данная функция нормируется для измерительных преобразователей и приборов с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины. Она задается в виде формулы, таблицы или графика и используется для определения значений измеряемой величины Х в рабочих условиях применения средств измерений по известному значению информативного параметра его выходного сигнала: Х = F-1(Y), F-1 – функция, обратная функции преобразования; Y – показания средства измерений;
— значение Y однозначной или значение Yi многозначной меры. Для этих характеристик нормируются номинальные или индивидуальные значения. Они используются для устройств, применяемых в качестве мер;
— цена деления шкалы измерительного прибора или многозначной меры. Нормирование цены деления производится для показывающих приборов с равномерной шкалой, функция преобразования которых отображается на именованной шкале. При неравномерной шкале нормируется минимальная цена деления;
— характеристики цифрового кода, используемого в средствах измерений и их элементах.К ним относятся: вид выходного кода, число его разрядов, цена единицы младшего разряда. Эти характеристики нормируются для цифровых приборов.
Точностные характеристики средства измерений– совокупность метрологических характеристик средства измерений, влияющих на погрешность измерения. К точностным характеристикам относят погрешность средства измерении, нестабильность, порог чувствительности, дрейф нуля и др.
Рассмотрим одну из таких характеристик – чувствительность средства измерений.
Чувствительность средства измерений – свойство средства измерений, определяемое отношением изменения выходного сигнала этого средства к вызывающему его изменению измеряемой величины. Различают абсолютную и относительную чувствительность. Абсолютную чувствительность определяют по формуле:
S = Dl / Dx, (6.7)
относительную чувствительность – по формуле:
S0 =Dl / Dx / x, (6.8)
где D1 – изменение сигнала на выходе;
х – измеряемая величина;
Dх – изменение измеряемой величины.
Порог чувствительности средства измерений– характеристика средства измерений в виде наименьшего значения изменения физической величины, начиная с которого может осуществляться ее измерение данным средством.
Определение погрешности
Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.


Необходимо отметить, что таким способом можно посчитать только основную погрешность.
Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.
Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений.
Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.
Источник:
Выбор амперметра по метрологическим характеристикам
Наиболее частым источником ошибки при измерении тока считается то, что амперметр имеет ненулевое входное сопротивление. Напряжение, возникающее на измерителе, приводит к снижению напряжения на тестируемом устройстве. Если уменьшение будет значительным, это приведет к значительно меньшему протеканию тока. Другими словами, измеритель не показывает ток, который фактически протекает в сети.
Для того чтобы максимально нивелировать эту погрешность, применяют два основных типа архитектуры измерения: шунтирующие амперметры и с обратной связью.
Погрешность, вызванная шунтирующим измерителем, определяемая в виде частного напряжения амперметра, деленная на выходное сопротивление.
Амперметры с обратной связью ближе к «идеальным». Он вырабатывает напряжение на пути обратной связи операционного усилителя с высоким коэффициентом усиления. Это напряжение также пропорционально измеряемому току, но не появляется на входе прибора. В результате чувствительные измерители с обратной связью, такие как электрометры и пикоамперметры, имеют нагрузку по напряжению, обычно ограниченную до 200 мкВ.
Для промышленных измерений наиболее часто применяются амперметры аналогового панельного типа. При их выборе следует учитывать такие моменты:
- Выбор типа. При измерении І постоянного, следует выбрать измеритель постоянного тока, то есть с магнитоэлектрическим измерительным механизмом. При измерении переменного тока нужно обратить внимание на форму волны и частоту. Если это синусоида, то измеряют только эффективное значение, с последующим преобразованием в максимальное или среднее значение.
- Класс точности. Чем более высокий класс точности измерителя, тем выше его цена, тем сложнее у него ремонт и метрологическая аттестация. Поэтому для выполнения большинства инженерных измерений достаточно класса точности 1.5, не стоит применять образцовые или лабораторные приборы.
- Выбор шкалы. Чтобы в полной мере использовать возможности амперметра по классу точности, измеряемый показатель должен быть в интервале 1/2
Важно! Внутреннее сопротивление — определяющая величина при выборе измерителя. Ее следует принимать в соответствии с величиной измеряемого импеданса, иначе это приведет к большим ошибкам измерения. Поскольку внутреннее сопротивление отражает энергопотребление самого измерителя, при измерении тока прибор с внутренним сопротивлением следует выбирать, как можно меньшим.