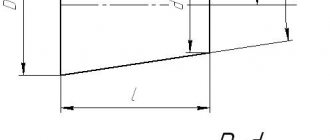
Нормальные утлы (по ГОСТ 8908-81)
| 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд |
| 0° | 10° | 70° | ||||||
| 0°15′ | 12° | 75° | ||||||
| 0°30′ | 15° | 80 | ||||||
| 0º45′ | 18 | 85 | ||||||
| 1° | 20 | 90° | ||||||
| 1°30′ | 22 | 100 | ||||||
| 2 | 25 | 110 | ||||||
| 2°30′ | 30 | 120 | ||||||
| 3 | 35 | 135 | ||||||
| 4 | 40 | 150 | ||||||
| 5 | 5 | 45 | 165 | |||||
| 6 | 50 | 180 | ||||||
| 7 | 55 | 270 | ||||||
| 8 | 60 | 360 | ||||||
| 9 | 65 |
Таблица не распространяется на угловые размеры конусов.
При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
Нормативные требования по уклонам
При проектировании улиц населенных пунктов необходимо соблюдать требования по минимальным и максимальным показателям продольных и поперечных уклонов. Значения уклонов приводятся в промилле.
Поперечный уклон проезжей части улиц и площадей принимается в зависимости от типа дорожного покрытия:
— асфальтобетонные и цементобетонные – 15 ‰ — 25 ‰;
— сборные из бетонных и железобетонных плит, брусчатые мостовые — 20 ‰ — 25 ‰;
— щебеночные и гравийные — 20 ‰ — 30 ‰;
— булыжные мостовые — 20 ‰ — 35 ‰.
При возведении и реконструкции в стесненных условиях можно увеличить поперечные уклоны на 5 ‰.
Поперечные и продольные уклоны машино-места на площадках автостоянок и парковок принимается в пределах от 5 ‰ до 40 ‰.
Поперечный уклон машино-места на парковках, прилегающих непосредственно к проезжей части улиц, допускается увеличивать до 60 ‰.
Минимальный продольный уклон на улицах со стоком поверхностных вод, осуществляемым
по лоткам вдоль проезжей части, следует принимать:
— для асфальтобетонных и цементобетонных покрытий — 4 ‰;
— для остальных типов покрытий — 5 ‰.
Если водоотводные лотки вдоль проезжей части не предусматриваются, то значение минимального продольного уклона не нормируется, и он обеспечивается за счет поперечных уклонов.
Продольные уклоны на участках улиц с движением автобусов, троллейбусов и трамваев не должны превышать:
— 60 ‰ — с остановочными пунктами и радиусами кривых в плане 250 м и более;
— 40 ‰ — с остановочными пунктами и радиусами кривых в плане от 100 до 250 м;
— 40 ‰ — без остановочных пунктов с радиусами кривых в плане менее 100 м.
Нормальные конусности и углы конусов (по ГОСТ 8593-81)
Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.
C = (D — d) / L = 2tg(α/2)
| Обозначение конуса | КонусностьC | Угол конуса α | Угол уклона α / 2 | ||||
| ряд 1 | ряд 2 | утл.ед. | рад | утл.ед. | рад | ||
| 1 : 500 | 1 : 500 | 0,0020000 | 6’52,5″ | 0,0000 | 3’26,25″ | 0,0010000 | |
| 1 :200 | 1 : 200 | 0,0050000 | 1711,3″ | 0,0050000 | 8’35,55″ | 0,0025000 | |
| 1 : 100 | 1 : 100 | 0,0100000 | 34’22,6″ | 0,0100000 | 17’11,3» | 0,0050000 | |
| 1 : 50 | 1 : 50 | 0,0200000 | 1°8’45,2″ | 0,0199996 | 34’22,6″ | 0,0099998 | |
| 1 : 30 | 1 :30 | 0,0333333 | 1°54’31,9″ | 0,0333304 | 57’17,45″ | 0,0166652 | |
| 1 : 20 | 1 :20 | 0,0500000 | 2°51’51,1» | 0,0499896 | 1°25’55,55″ | 0,0249948 | |
| 1 : 15 | 1 : 15 | 0,0666667 | 3°49’5,9″ | 0,0666420 | 1°54’32,95″ | 0,0333210 | |
| 1 : 12 | 1 : 12 | 0,0833333 | 4°4618,8″ | 0,0832852 | 2°23’19,4″ | 0,0416426 | |
| 1 : 10 | 1 : 10 | 0,1000000 | 5°43’29,3″ | 0,0999168 | 2°5144,65″ | 0,0499584 | |
| 1 : 8 | 1 : 8 | 0,1250000 | 7°9’9,6″ | 0,1248376 | 3°34’34,8″ | 0,0624188 | |
| 1 : 7 | 1 :7 | 0,1428571 | 8°10’16,4″ | 0,1426148 | 4°5’8,2″ | 0,0713074 | |
| 1 : 6 | 1 :6 | 0,1666667 | 9°31’38,2″ | 0,1662824 | 4°45’49,1» | 0,0831412 | |
| 1 : 5 | 1 :5 | 0,2000000 | 11°25’16,3″ | 0,1993374 | 5º42’38,15″ | 0,0996687 | |
| 1 : 4 | 1 : 4 | 0,2500000 | 14°15’0,1» | 0,2487100 | 7°7’30,05″ | 0,1243550 | |
| 1 : 3 | 1 : 3 | 0,3333333 | 18°55’28,7″ | 0,3302972 | 9°27’44,35″ | 0,1651486 | |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 | |
| 45е | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30′ | 0,3926991 | |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 | |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30′ | 0,6544985 | |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 | |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 | |
Примечание.
Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице.
При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Преобразование процентов

1
Переместите десятичную запятую на две позиции влево.
Это приведет к преобразованию процентов в десятичную дробь. Если в процентном числе десятичная запятая отсутствует, смело ставьте ее после последней цифры, например, 75% = 75,0%. Переместите десятичную запятую на две позиции влево, чтобы преобразовать проценты в десятичную дробь – это аналогично делению числа на 100. Например:[1]
- 75% = 0,75
3,1% = 0,031
- 0,5% = 0,005


2
Выразите проценты как долю от 100.
Вы можете представить проценты в виде обыкновенной дроби со знаменателем 100, при этом в числителе записывается процентное число. Затем нужно упростить полученную дробь (если, конечно, это возможно).
- Например, 36% = 36/100.
Для упрощения дроби найдите наибольшее число, на которое делится и числитель, и знаменатель. В нашем примере таким числом является число 4.
- Разделите и числитель, и знаменатель на найденное число. В нашем примере вы получите: 36/100 = 9/25.
- Для проверки ответа разделите числитель на знаменатель: 9 ÷ 25 = 0,36, а затем результат умножьте на 100: 0,36 х 100 = 36%. Полученное число должно быть равно процентному числу.


3
Избавьтесь от знака процентов.
Преобразовав проценты в обыкновенную или десятичную дробь, знак процентов (%) больше не нужен. Помните, что проценты – это некоторая доля от 100, поэтому если вы забудете убрать знак процентов после преобразования в десятичную дробь, то это будет означать, что ваш ответ является долей от 100.[2]
Конусность наружных и внутренних конусов с резьбовым отверстием
| Обозначение величины конуса | Конусность | Угол конуса 2α |
| В7 | 1 : 19,212 = 0,05205 | 2°58’54» |
| B10; B12 | 1 : 20,047 = 0,4988 | 2°51’26» |
| В16; В18 | 1 : 20, = 0,04995 | 2°51’41» |
| В22; В24 | 1 : 19,922 = 0,05020 | 2°52’32» |
| В32 | 1 : 19,954 = 0,05194 | 2º58’31» |
| В45 | 1 : 19,002 = 0,05263 | 3°00’53» |
Угол конуса 2α подсчитан по величине конусности с округлением 1»
Рекомендуемые размеры центрового отверстия укороченного конуса
Размеры, мм
Центровые отверстия для конусов Морзе В12, В18, В24 и В45 — формы Р по ГОСТ 14034-74. Допускается изготовление центрового отверстия с размерами, указанными в таблице.
| Обозначение конуса Морзе | d2 | d3 | d4 | L |
| В12 | М6 | 8,0 | 8,5 | 16 |
| В18 | М10 | 12,5 | 13,2 | 24 |
| В24 | М12 | 15,0 | 17,0 | 28 |
| В32 В45 | М16 М20 | 20,0 26,0 | 22,0 30,0 | 32 40 |
Преобразование обыкновенных дробей

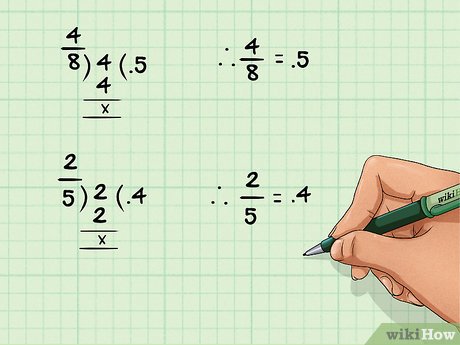
1
Для преобразования обыкновенной дроби в десятичную просто разделите числитель на знаменатель.
Помните, что черта между числителем и знаменателем означает операцию деления. То есть дробь х/у – это «х», деленный на «у».[7]
- Например: дробь 4/8 = 0,5.


2
Определитесь с количеством знаков (цифр) после десятичной запятой.
Многие числа на делятся нацело. Разделив такие числа, оставьте определенное количество знаков после запятой. В большинстве случаев после запятой можно оставить два знака. Запомните правила округления: если после округляемого знака стоит цифра от 5 до 9, то округляемая цифра увеличивается на 1; в противном случае округляемая цифра не меняется. Например, дробь 0,145 округляется до 0,15.
- Например, 5/17 = 0,2941176470588 …
Здесь округленная дробь равна 0,29.

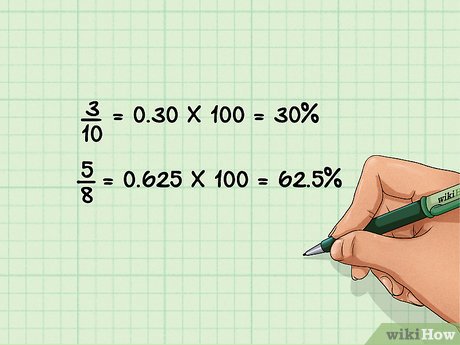
3
Разделите числитель на знаменатель, а затем полученный результат умножьте на 100, чтобы получить проценты.
Разделите числитель обыкновенной дроби на ее знаменатель, полученный результат умножьте на 100, к ответу припишите знак процентов (%), и вы получите проценты.[8]
- Например, дана дробь 4/8. Разделите 4 на 8 и получите 0,50. Умножьте 0,50 на 100 и получите 50. Припишите знак процентов и получите окончательный ответ: 50%.
Дополнительные примеры: 3/10 = 0,30 * 100 = 30%
- 5/8 = 0,625 * 100 = 62,5%
Размеры, мм
Внутренние конусы
Для конусов с лапкой
Для конусов с резьбовым отверстием
| Конус | Метрический | Морзе | Метрический | |||||||||||
| Обозначение конуса | 4 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 80 | 100 | 120 | 160 | 200 |
| Конусность | 1 : 20 = 0,05 | 1 : 19,212 = 0,05205 | 1 : 20,047 = 0,04988 | 1 : 20,020 = 0,04995 | 1 : 19,922 = 0,05 | 1 : 19,254 = 0,05194 | 1 : 19,002 = 0,05263 | 1 : 19,180 = 0,05214 | 1 : 20 = 0,05 | |||||
| D | 4 | 6 | 9,045 | 12,065 | 17,780 | 23,825 | 31,267 | 44,399 | 63,348 | 80 | 100 | 120 | 160 | 200 |
| d5 | 3 | 4,6 | 6,7 | 9,7 | 14,9 | 20,2 | 26,5 | 38,2 | 54,6 | 71,5 | 90 | 108,5 | 145,5 | 182,5 |
| d6 | — | — | — | 7 | 11,5 | 14 | 18 | 23 | 27 | 33 | 39 | 52 | ||
| l5 min | 25 | 34 | 52 | 56 | 67 | 84 | 107 | 135 | 188 | 202 | 240 | 276 | 350 | 424 |
| l6 | 21 | 29 | 49 | 52 | 62 | 78 | 98 | 125 | 177 | 186 | 220 | 254 | 321 | 388 |
| g | 2,2 | 3,2 | 3,9 | 5,2 | 6,3 | 7,9 | 11,9 | 15,9 | 19 | 26 | 32 | 38 | 50 | 62 |
| h | 8 | 12 | 15 | 19 | 22 | 27 | 32 | 38 | 47 | 52 | 60 | 70 | 90 | 110 |
1. ГОСТ предусматривает размеры и для конусов инструментальных наружных.
2. Предельные отклонения размеров конусов и допуски формы по ГОСТ 2848-75.
Преобразование десятичных дробей


1
Умножьте десятичную дробь на 100, чтобы получить проценты.
Или просто переместите десятичную запятую на две позиции вправо. Помните, что проценты – это некоторая доля от 100, поэтому, умножив десятичную дробь на 100, вы получите эту «долю от 100». После умножения не забудьте приписать знак процентов (%).[3] Например: 0,32 = 32%; 0,07 = 7%; 1,25 = 125%; 0,083 = 8,3%


2
Преобразуйте конечную десятичную дробь в обыкновенную дробь.
Конечная десятичная дробь после десятичной запятой имеет ограниченное количество цифр. Переместите десятичную запятую на количество позиций вправо, равное количеству цифр после десятичной запятой. Полученное число – это числитель обыкновенной дроби. В знаменателе напишите 1 с количеством нулей, равным количеству цифр после десятичной запятой. Затем нужно упростить полученную дробь (если, конечно, это возможно).[4]
- Например, в десятичной дроби 0,32 после запятой две цифры. Переместите десятичную запятую на две позиции вправо, а в знаменателе запишите 100; таким образом, 0,32 = 32/100. Разделите и числитель, и знаменатель на 4 и получите: 36/100 = 9/25.
Другой пример: в десятичной дроби 0,8 после запятой одна цифра. Переместите десятичную запятую на одну позицию вправо, а в знаменателе запишите 10; таким образом, 0,8 = 8/10. Разделите и числитель, и знаменатель на 2 и получите: 8/10 = 4/5.
- Для проверки ответа просто разделите числитель на знаменатель – результат должен быть равен исходной десятичной дроби. В нашем примере: 8/25 = 0,32.


3
Преобразуйте периодическую дробь в обыкновенную дробь.
Периодическая дробь после десятичной запятой имеет периодически повторяющуюся группу цифр. Например, в дроби 0,131313… периодически повторяются две цифры (13). Определите, сколько цифр периодически повторяются, а затем умножьте периодическую дробь на 10n, где n – это количество периодически повторяющихся цифр.[5]
- В нашем примере 0,131313… умножьте на 100 (10 во второй степени) и получите 13,131313…
Для нахождения числителя (верхнее число) обыкновенной дроби из полученной дроби вычтите повторяющуюся группу цифр. В нашем примере: 13,131313… – 0,131313… = 13, то есть числитель равен 13.[6]
- Для нахождения знаменателя (нижнее число) из числа, на которое вы умножали исходную периодическую дробь, вычтите 1. Например, вы умножали исходную дробь 0,131313… на 100, поэтому знаменатель равен 100 – 1 = 99.
- В нашем примере: 0,131313…= 13/99.
- Дополнительные примеры: 0,333… = 3/9
- 0,123123123… = 123/999
- 0,142857142857… = 142857/999999
- В случае необходимости упростите дробь, например, 142857/999999 = 1/7.
Конусы внутренние и наружные конусностью 7 : 24 (по ГОСТ 15945-82)
Размеры, мм
Пример обозначения конуса 25:
Конус 25 ГОСТ 15945-82
| Обозначение конуса | D | L* (справочный) |
| 10 | 15,87 | 21,8 |
| 15 | 19,05 | 26,9 |
| 25 | 25,40 | 39,8 |
| 30 | 31,75 | 49,2 |
| 35 | 38,10 | 57,2 |
| 40 | 44,45 | 65,6 |
| 45 | 57,15 | 84,8 |
| 50 | 69,85 | 103,7 |
| 55 | 88,90 | 131,6 |
| 60 | 107,95 | 163,7 |
| 65 | 133,35 | 200,0 |
| 70 | 165,10 | 247,5 |
| 75 | 203,20 | 305,8 |
| 80 | 254,00 | 390,8 |
Размеры и допуски углов наружных и внутренних конусов
* Размер для справок.
** Z — базорасстояние конуса задается в стандартах на конкретную продукцию
1 — основная плоскость; 2 — базовая плоскость
| Обозначения конусов | D | d | Lрасч | Допуск угла, мкм, конуса ATDпо ГОСТ 8908 | ||||
| 3 | 4 | 5 | 6 | 7 | ||||
| 30 | 31,75 | 17,750 | 48 | 2,5 | 4 | 6 | 10 | 15 |
| 35 | 38,10 | 21,767 | 56 | 2,5 | 4 | 6 | 10 | 15 |
| 40 | 44,45 | 25,492 | 65 | 3,0 | 5 | 8 | 12 | 20 |
| 45 | 57,15 | 32,942 | 83 | 3,0 | 5 | 8 | 12 | 20 |
| 50 | 69,85 | 40,100 | 102 | 4,0 | 6 | 10 | 16 | 25 |
| 55 | 88,90 | 54,858 | 127 | 4,0 | 6 | 10 | 16 | 25 |
| 60 | 107,95 | 60,700 | 162 | 5,0 | 8 | 12 | 20 | 30 |
| 65 | 133,35 | 74,433 | 202 | 5,0 | 8 | 12 | 20 | 30 |
| 70 | 165,10 | 92,183 | 250 | 6,0 | 10 | 16 | 25 | 40 |
| 75 | 203,20 | 113,658 | 307 | 6,0 | 10 | 16 | 25 | 40 |
| 80 | 254,00 | 138,208 | 394 | 8,0 | 12 | 20 | 30 | 50 |
Условное обозначение конусов по ГОСТ 15945 с добавлением степени точности конуса:
Конус 50 АТ5 ГОСТ 15945-82
Предельные отклонения базорасстояния конуса Z следует выбирать из ряда: ± 0,4; ± 0,2; ± 0,1; ± 0,05мм.
Продолжение табл. 10
Поручни для пандуса


- В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.
- Верхний поручень расположен на высоте 900 мм.
- Расстояние между поручнями 900-1000 мм.
- Перила должны быть круглого сечения с диаметром от 30 до 50 мм.
- Начало и конец маркируются предупредительными полосами.
- Нижний поручень должен быть на высоте 700 мм.
- По продольным краям марша пандуса следует устанавливать бортики высотой не менее 0,05 м.
- Покрытие пандуса должно обладать противоскользящим эффектом.
- Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.
- Поручни с внутренней стороны не должны прерываться.
- Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.
Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:
- Опорными поручнями. Расстояние между поручнями пандуса одностороннего движения должно быть в пределах 0,9-1,0 м, чтобы инвалид-колясочник мог на них подтянуться. Также для удобства и безопасности хвата поручни должны иметь закругленную форму и выступать на 300 мм от края.
- Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.
Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.


Вопросы по адаптации Автопарковка для МГН Адаптация тротуаров для незрячих Адаптация лестниц для МГН Адаптация входной группы Адаптация холла в помещении Адаптация санузела для незрячих Адаптация лифтов для МГН