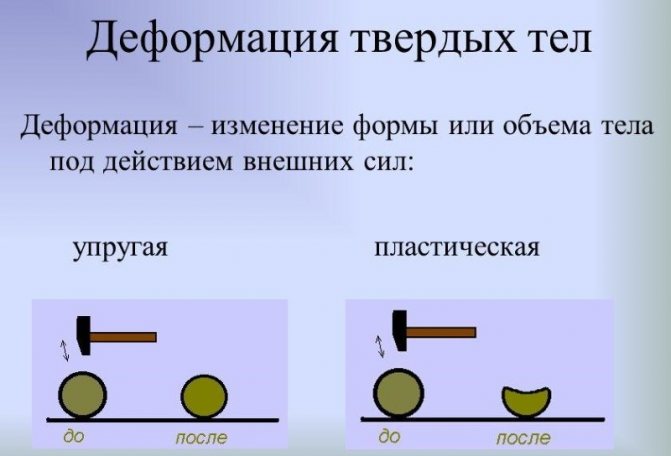
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Применение эффекта Пуассона [ править ]
Одна из областей, на которую эффект Пуассона оказывает значительное влияние, — это поток в трубе под давлением. Когда воздух или жидкость внутри трубы находятся под высоким давлением, они оказывают равномерное усилие на внутреннюю часть трубы, что приводит к кольцевому напряжению внутри материала трубы. Из-за эффекта Пуассона это кольцевое напряжение приведет к увеличению диаметра трубы и небольшому уменьшению ее длины. Уменьшение длины, в частности, может оказать заметное влияние на стыки труб, так как эффект будет накапливаться для каждой секции трубы, соединенной последовательно. Сдерживаемый сустав может быть растянут или иным образом подвержен поломке. [ необходима цитата
]
Другая область применения эффекта Пуассона — это структурная геология . Камни, как и большинство материалов, подвержены эффекту Пуассона при напряжении. В геологическом масштабе времени чрезмерная эрозия или осаждение земной коры может создавать или снимать большие вертикальные напряжения на подстилающей породе. Эта порода будет расширяться или сжиматься в вертикальном направлении в результате приложенного напряжения, а также будет деформироваться в горизонтальном направлении в результате эффекта Пуассона. Это изменение деформации в горизонтальном направлении может повлиять на соединения и спящие напряжения в породе или образовать их. [29]
Хотя исторически пробка использовалась для герметизации винных бутылок по другим причинам (включая ее инертную природу, непроницаемость, гибкость, герметизирующую способность и упругость) [30] , нулевой коэффициент Пуассона пробки дает еще одно преимущество. Когда пробка вставляется в бутылку, верхняя часть, которая еще не вставлена, не расширяется в диаметре, поскольку сжимается в осевом направлении. Сила, необходимая для того, чтобы вставить пробку в бутылку, возникает только из-за трения между пробкой и бутылкой из-за радиального сжатия пробки. Если бы стопор был изготовлен, например, из резины (с коэффициентом Пуассона около 1/2), то для преодоления радиального расширения верхней части резинового стопора потребовалась бы относительно большая дополнительная сила.
Большинство автомехаников знают, что трудно снять резиновый шланг (например, шланг охлаждающей жидкости) с металлического отрезка трубы, так как натяжение натяжения приводит к уменьшению диаметра шланга, плотно сжимая отрезок. Шланги легче снимать с концов с помощью широкого плоского лезвия.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Читать также: Обмотку низшего напряжения трансформатора делают из сечения
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.


Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
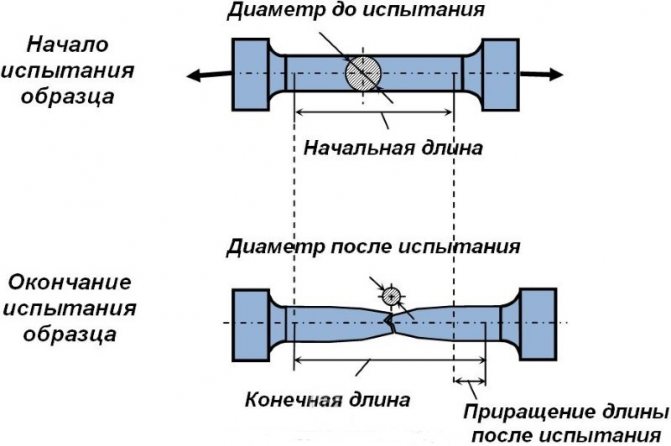

Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.


Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Физические характеристики алюминия
Модуль упругости Е, МПа (кгс/см 2 ), при температуре, °С:
от минус 40 до плюс 50
Модуль сдвига G,
МПа (кгс/см 2 ). при температуре, °С:
от минус 40 до плюс 50
Коэффициент поперечной деформации (Пуассона) г
Коэффициент линейного расширения а, °С”, при температуре от минус 70 до плюс 100°С
Среднее значение плотности р,
кг/м
Примечание. Для промежуточных значений температуры значения Е
и
G
следует определять линейной интерполяцией.
Плотность, кг/м 3
Алюминиевые полуфабрикаты, применяемые для строительных конструкций
Примечание. Знак „+» означает, что данный полуфабрикат применяется для строительных конструкций; знак „-» – данный полуфабрикат не применяется.
КОЭФФИЦИЕНТЫ ПРОДОЛЬНОГО ИЗГИБА ЦЕНТРАЛЬНО-СЖАТЫХ ЭЛЕМЕНТОВ
В табл. 1 показаны схемы сечения, для которых в табл. 2 и 3 настоящего приложения приведены значения коэффициента .
Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.
Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.
Содержание
- 1 Происхождение
- 2 Коэффициент Пуассона от изменений геометрии 2.1 Изменение длины
- 2.2 Изменение объема
- 2.3 Изменение ширины
- 3.1 Изотропный
- 4.1 Материалы с отрицательным коэффициентом Пуассона
Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Читать также: Обрезиненные ролики для станков
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
Опыт с пружинными весами
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Функция Пуассона [ править ]
При конечных деформациях , соотношение между поперечным и осевыми деформациями и , как правило , не очень хорошо описывается отношением Пуассона. Фактически, коэффициент Пуассона часто считается функцией приложенной деформации в режиме большой деформации. В таких случаях коэффициент Пуассона заменяется функцией Пуассона, для которой существует несколько конкурирующих определений. [28] Определение поперечного растяжения и осевого растяжения , где поперечное растяжение является функцией осевого растяжения (т. Е.), Наиболее распространенными являются функции Хенки, Био, Грина и Альманси. ε trans {\displaystyle \varepsilon _{\text{trans}}} ε axial {\displaystyle \varepsilon _{\text{axial}}} λ trans = ε trans + 1 {\displaystyle \lambda _{\text{trans}}=\varepsilon _{\text{trans}}+1} λ axial = ε axial + 1 {\displaystyle \lambda _{\text{axial}}=\varepsilon _{\text{axial}}+1} λ trans = λ trans ( λ axial ) {\displaystyle \lambda _{\text{trans}}=\lambda _{\text{trans}}(\lambda _{\text{axial}})}
ν Hencky = − ln λ trans ln λ axial ν Biot = 1 − λ trans λ axial − 1 ν Green = 1 − λ trans 2 λ axial 2 − 1 ν Almansi = λ trans − 2 − 1 1 − λ axial − 2 {\displaystyle {\begin{aligned}\nu ^{\text{Hencky}}&=-{\frac {\ln \lambda _{\text{trans}}}{\ln \lambda _{\text{axial}}}}\\[2pt]\nu ^{\text{Biot}}&={\frac {1-\lambda _{\text{trans}}}{\lambda _{\text{axial}}-1}}\\[2pt]\nu ^{\text{Green}}&={\frac {1-\lambda _{\text{trans}}^{2}}{\lambda _{\text{axial}}^{2}-1}}\\[2pt]\nu ^{\text{Almansi}}&={\frac {\lambda _{\text{trans}}^{-2}-1}{1-\lambda _{\text{axial}}^{-2}}}\end{aligned}}}
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
- Через касательные напряжения (τz) и угол сдвига (γ):
- Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
Ссылки [ править ]
- Для мягких материалов модуль объемной упругости (K) обычно больше по сравнению с модулем сдвига (G), так что их можно рассматривать как несжимаемые, поскольку легче изменить форму, чем сжать. Это приводит к модулю Юнга (Е) являетсяиследовательно. Ястшебский Д. (1959). Природа и свойства инженерных материалов
(изд. Wiley International). John Wiley & Sons, Inc. E = 3 G {\displaystyle E=3G} ν = 0.5 {\displaystyle \nu =0.5} - Лейкс, Р. и Войцеховски, К.В., 2008. Отрицательная сжимаемость, отрицательный коэффициент Пуассона и стабильность. Physica Status Solidi (B), 245 (3), стр. 545-551.
- Герчек, Х. (январь 2007 г.). «Значения коэффициента Пуассона для горных пород». Международный журнал механики горных пород и горных наук
.
44
(1): 1–13. DOI : 10.1016 / j.ijrmms.2006.04.011 . - Парк, RJT. Сейсмические характеристики стальных бетонных свай
- Марк, Шенк (2011). Складчатые конструкции оболочки, кандидатская диссертация
(PDF) . Кембриджский университет, Клэр-колледж. - Вэй, З.Ы .; Guo, ZV; Dudte, L .; Liang, HY; Махадеван, Л. (21 мая 2013 г.). «Геометрическая механика периодического гофрированного оригами» (PDF) . Письма с физическим обзором
.
110
(21): 215501. arXiv : 1211.6396 . Bibcode : 2013PhRvL.110u5501W . DOI : 10.1103 / PhysRevLett.110.215501 . PMID 23745895 . S2CID 9145953 . - Эйдини, Марьям; Паулино, Глаусио Х. (2015). «Раскрытие свойств метаматериала в листах, сложенных зигзагообразно» . Успехи науки
.
1
(8): e1500224. arXiv : 1502.05977 . Bibcode : 2015SciA …. 1E0224E . DOI : 10.1126 / sciadv.1500224 . ISSN 2375-2548 . PMC 4643767 . PMID 26601253 . - Eidini, Марьям (2016). «Листовые ячеистые механические метаматериалы, гнутые зигзагообразно». Письма об экстремальной механике
.
6
: 96–102. arXiv : 1509.08104 . DOI : 10.1016 / j.eml.2015.12.006 . S2CID 118424595 . - Мусанежад, Давуд; Бабай, Сахаб; Эбрахими, Хамид; Гош, Ранаджай; Хамуда, Абдельмагид Салем; Бертольди, Катя; Вазири, Ашкан (16 декабря 2015 г.). «Иерархические сотовые ауксетические метаматериалы» . Научные отчеты
.
5
: 18306. Bibcode : 2015NatSR … 518306M . DOI : 10.1038 / srep18306 . ISSN 2045-2322 . PMC 4680941 . PMID 26670417 . - https://arxiv.org/ftp/arxiv/papers/1204/1204.3859.pdf — Пределы коэффициента Пуассона в изотропных материалах — общий результат для произвольной деформации.
- Епишин, AI; Лисовенко, Д.С. (2016). «Экстремальные значения коэффициента Пуассона кубических кристаллов». Техническая физика
.
61
(10): 1516–1524. Bibcode : 2016JTePh..61.1516E . DOI : 10.1016 / j.mechmat.2019.03.017 . - Городцов, В.А.; Лисовенко Д.С. (2019). «Экстремальные значения модуля Юнга и коэффициента Пуассона гексагональных кристаллов». Механика материалов
.
134
: 1–8. DOI : 10.1016 / j.mechmat.2019.03.017 . - Boresi, А. Р, Шмидт, RJ и Sidebottom О.М., 1993, Advanced механика материалов
, Wiley. - Лехницкий С.Г., (1963), Теория упругости анизотропного упругого тела
, Holden-Day Inc. - Тан, SC, 1994, Концентрации напряжений в ламинированных композитах
, Technomic Publishing Company, Ланкастер, Пенсильвания. - Флюгель, Александр. «Расчет коэффициента Пуассона для очков» . www.glassproperties.com
. Архивировано 23 октября 2022 года . Проверено 28 апреля 2018 . - «Архивная копия» (PDF) . Архивировано (PDF) из оригинала 31.10.2014 . Проверено 24 сентября 2014 . CS1 maint: archived copy as title (link)
- Журнал прикладной физики 110, 053521 (2011)
- Лейкс, Род. «Отрицательный коэффициент Пуассона» . silver.neep.wisc.edu
. Архивировано 16 февраля 2022 года . Проверено 28 апреля 2018 . - Озихар, Томаш; Геринг, Стефан; Немц, Питер (март 2013). «Вязкоупругие характеристики древесины: зависимость ортотропной податливости при растяжении и сжатии от времени». Журнал реологии
.
57
(2): 699–717. Bibcode : 2013JRheo..57..699O . DOI : 10.1122 / 1.4790170 . ISSN 0148-6055 . - Цзян, Цзяли; Эрик Валентин, Бахтияр; Лу, Цзяньсюн; Немц, Питер (2016-11-01). «Временная зависимость модулей ортотропного сжатия Юнга и коэффициентов Пуассона древесины пихты китайской» (PDF) . Holzforschung
.
70
(11): 1093–1101. DOI : 10,1515 / ВЧ-2016-0001 . ISSN 1437-434X . S2CID 137799672 . - Carta, Джорджио; Брун, Мишель; Бальди, Антонио (2016). «Конструкция пористого материала с изотропным отрицательным коэффициентом Пуассона». Механика материалов
.
97
: 67–75. DOI : 10.1016 / j.mechmat.2016.02.012 . - Кабрас, Луиджи; Брун, Мишель (2016). «Класс ауксетических трехмерных решеток» . Журнал механики и физики твердого тела
.
91
: 56–72. arXiv : 1506.04919 . Bibcode : 2016JMPSo..91 … 56C . DOI : 10.1016 / j.jmps.2016.02.010 . S2CID 85547530 . - Кабрас, Луиджи; Брун, Мишель (2014). «Ауксетические двумерные решетки с коэффициентом Пуассона, сколь угодно близким к -1». Труды Королевского общества А
.
470
(2172): 20140538. arXiv : 1407.5679 . Bibcode : 2014RSPSA.47040538C . DOI : 10,1098 / rspa.2014.0538 . S2CID 119321604 . - Гольдштейн, Р.В.; Городцов В.А.; Лисовенко, Д.С. (2013). «Классификация кубических ауксетиков». Physica Status Solidi B
.
250
(10): 2038–2043. DOI : 10.1002 / pssb.201384233 . - Гольдштейн, Р.В.; Городцов В.А.; Лисовенко, Д.С. (2011). «Изменчивость упругих свойств гексагональных ауксетиков». Доклады Физики
.
56
(12): 602–605. DOI : 10.1134 / S1028335811120019 . S2CID 120998323 . - Гольдштейн, Р.В.; Городцов В.А.; Лисовенко Д.С. Волков, М.А. (2015). «Ауксетики среди 6-константных тетрагональных кристаллов» . Письма о материалах
.
5
(4): 409–413. DOI : 10.22226 / 2410-3535-2015-4-409-413 . - Михай, Луизиана; Гориели, А. (03.11.2017). «Как охарактеризовать нелинейный упругий материал? Обзор нелинейных определяющих параметров в изотропной конечной упругости» . Труды Королевского общества А
.
473
(2207): 20170607. Bibcode : 2017RSPSA.47370607M . DOI : 10,1098 / rspa.2017.0607 . PMC 5719638 . PMID 29225507 . - «Конспект лекций по структурной геологии — эффективное напряжение» . Проверено 3 июля 2022 .
- Сильва и др. «Корк: свойства, возможности и приложения». Архивировано 9августа 2022 г.в Wayback Machine. Проверено 4 мая 2017 г.
Модуль упругости различных материалов
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
- природы веществ, формирующих состав материала;
- моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
- структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
- плотности материала (распределения частиц в его объеме);
- обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).
Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
- бронза – 10,4 ГПа;
- алюминиевая бронза при литье – 10,3 ГПа;
- фосфористая бронза катанная – 11,3 ГПа.
Читать также: Отверстие под резьбу м27
Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.
Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:
- литая – 82 ГПа;
- прокатанная – 108 ГПа;
- деформированная – 112 ГПа;
- холоднотянутая – 127 ГПа.
Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.
Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.
Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.
Модули упругости некоторых материалов
На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:
Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.
Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.
Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.
Сталь 45 конструкционная углеродистая качественная
Заменители
Иностранные аналоги
| Германия (DIN) | C45, C45E+QT, Ck45, Cm45 |
| Евронормы (EN) | 1.0503, 1.1191 |
| США | M1044, 1044, 1045, M1045 |
| Япония | S45C, S48C |
ВАЖНО. Возможность замены определяется в каждом конкретном случае после оценки и сравнения свойств сталей
Расшифровка
Цифра 45 указывает среднее содержание углерода в сотых долях процента, т.е. содержание углерода в стали 45 составляет 0,45%.
Характеристики и назначение
Сталь марки 45 относится к конструкционным углеродистым нелегированным специальным качественным сталям с нормальным содержанием марганца.
Сталь марки 45 применяется для изготовления:
- муфт насосных штанг,
- вал-шестерни,
- валов центробежных насосов,
- штоков грязевых насосов,
- пальцев крейцкопфов грязевых насосов,
- компрессоров,
- роторов,
- стволов и переводников вертлюгов,
- переводников для рабочих и бурильных труб,
- корпусов колонковых долот,
- роликов превентора,
- конических шестерен,
- шестерни,
- фиксаторов и шпонок буровых станков,
- цепных колес буровых лебедок,
- штифтов,
- упорных винтов,
- скалок насосов,
- цапф,
- коленчатые и распределительные валы,
- шпиндели,
- бандажи,
- цилиндры,
- кулачки,
- другие нормализованные, улучшаемые и подвергаемые поверхностной термообработке детали, от которых требуется повышенная прочность.
Применение стали 45 для деталей арматуры и пневмоприводов, не работающих под давлением и не подлежащих сварке, предназначенных для эксплуатации в условиях низких температур
| Марка стали | Закалка + отпуск при температуре, °С | Примерный уровень прочности, Н/мм2(кгс/мм2) | Температура применения не ниже,°С | Использование в толщине не более, мм |
| 45 | 500 | 900 (90) | -50 | 20 |
- При термической обработке на прочность ниже указанной в графе 3 или при использовании в деталях с толщиной стенки менее 10 мм температура эксплуатации может быть понижена.
- Максимальная толщина, указанная в графе 5, обусловлена необходимостью получения сквозной прокаливаемости и однородности свойств по сечению.
Применение стали 45 для изготовление крепежных деталей (ГОСТ 32569-2013)
| Марка стали | Технические требования | Допустимые параметры эксплуатации | Назначение | |
| Температура стенка, °С | Давление среды, МПа(кгс/см2), не более | |||
| Сталь 45 ГОСТ 1050 ГОСТ 10702 | СТП 26.260.2043 | От -40 до +425 | 10(100) | Шпильки, болты |
| 16(160) | Гайки | |||
| От -40 до +450 | Шайбы | |||
Пределы применения, виды обязательных испытаний и контроля стали 45 для фланцев для давление свыше 10 МПа (100 кгс/см2) (ГОСТ 32569-2013)
| Марка стали | Технические требования | Наименование детали | Предельные параметры | Обязательные испытания | Контроль | |||||||
| Температура стенка, °С не более | Давление номинальное, МПа(кгс/см2), не более | σ0,2, МПа | σв, МПа | δ5, % | ψ% | KCU, Дж/см2 | Твердость HB | Дефектоскопия | Неметаллические включения | |||
| Сталь 45 ГОСТ 1050 ГОСТ 10702 | ГОСТ 9399 | Фланцы | От -40 до +200 | 32(320) | 16(160) | + | + | + | + | + | + | — |
Стойкость стали 45 против щелевой эрозии
ПРИМЕЧАНИЕ. Коэффициент эрозионной стойкости материала представляет собой отношение скорости эрозионного износа материала к скорости эрозионного износа стали 12Х18Н10Т (принятой за 1).
Применение стали 45 для изготовления основных деталей арматуры АС
| Материал | Вид полуфабриката или изделия | Максимально допустимая температура применения, °С | |
| Наименование | Марка, НД на материал | ||
| Углеродистая сталь | Сталь 45 ГОСТ 1050 | Поковки, сортовой прокат. Крепеж | 350 |
Вид поставки
- сортовой прокат, в том числе фасонный: ГОСТ 1050-88, ГОСТ 2590-88, ГОСТ 2591-88, ГОСТ 2879-88, ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 8239-89, ГОСТ 8240-89, ГОСТ 10702-78.
- Калиброванный пруток ГОСТ 1050-74, ГОСТ 7417-75, ГОСТ 8559-75, ГОСТ 8560-78, ГОСТ 10702-78.
- Шлифованный пруток и серебрянка ГОСТ 14955-77, ГОСТ 10702-78.
- Лист толстый ГОСТ 1577-93, ГОСТ 19903-74.
- Лист тонкий ГОСТ 16523-89.
- Лента ГОСТ 2284-79.
- Полоса ГОСТ 1577-93, ГОСТ 103-76, ГОСТ 82-70.
- Проволока ГОСТ 17305-91, ГОСТ 5663-79.
- Поковки и кованые заготовки ГОСТ 8479-70, ГОСТ 1133-71.
- Трубы ГОСТ 8732-78, ГОСТ 8733-74, ГОСТ 8734-75, ГОСТ 8731-74, ГОСТ 21729-76.
Химический состав, % (ГОСТ 1050-88)
Химический состав, % (ГОСТ 1050-2013)
| Класс стали | Марка стали | Массовая доля элементов, % | |||||||
| C | Si | Mn | P | S | Cr | Ni | Cu | ||
| не более | |||||||||
| Нелегированные специальные | 45 | 0,42-0,50 | 0,17-0,37 | 0,50-0,80 | 0,030 | 0,035 | 0,25 | 0,30 | 0,30 |
Термообработка
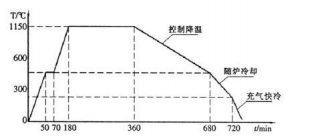
Детали из стали марки 45 подвергаются нормализации при температуре 860-880° С или закалке в воде с температуры 840-860° С с последующим отпуском; температура отпуска устанавливается в зависимости от требуемых механических свойств (рис. ниже).
Так, например, детали буровых установок (шестерни, фиксатор, шпонки) превентора (плита основной опоры, ролики) подвергаются отпуску при температуре 550° С, цепные колеса буровой лебедки — при температуре 500 С.
Влияние азотирования на предел выносливости стали 45
Для деталей, работающих на износ при невысоких контактных нагрузках, углеродистую сталь марки 45 упрочняют по кратковременным режимам азотирования (520—570 °С, Выдержка 1-6 ч). При этом, несмотря на небольшое увеличение твердости, обеспечивается повышение антифрикционных свойств, сопротивления знакопеременным нагрузкам и коррозии.
| Марка стали | Тип образца | Предел выносливости, кгс/мм2 | |
| после улучшения | после азотирования | ||
| 45 | Гладкий, d = 7,5 мм | 44 | 61 |
- Азотирование проводилось при 520-540°С, глубина слоя 0,35-0,45 мм.
- На образцах диаметром 7,5 мм надрез с углом 60° и глубиной 0,3 мм.
Твердость закаленного слоя после отпуска HRCэ при высокочастотной закалке
Температура критических точек, °С
Твердость HB (по Бринеллю) для металлопродукции из стали 45 (ГОСТ 1050-2013)
| Марка стали | не более | |||
| горячекатаной и кованой | калиброванной и со специальной отделкой поверхности | |||
| без термической обработки | после отжига или высокого отпуска | нагартованной | после отжига или высокого отпуска | |
| 45 | 229 | 197 | 241 | 207 |
Твердость на закаленных образцах HRC (по Роквеллу) (ГОСТ 1050-2013)
Механические свойства проката
| Гост | Состояние поставки | Сечение, мм | σв, МПа | δ5(δ4), % | ψ% |
| не менее | |||||
| ГОСТ 1050-88 | Сталь горячекатаная, кованая, калиброванная и серебрянка 2-й категории после нормализации | 25 | 600 | 16 | 40 |
| Сталь калиброванная 5-й категории после нагартовки | Образцы | 640 | 6 | 30 | |
| ГОСТ 10702-78 | Сталь калиброванная и калиброванная со специальной отделкой после отпуска или отжига | — | До 590 | — | 40 |
| ГОСТ 1577-93 | Лист нормализованный и горяче- катаный | 80 | 590 | 18 | — |
| Полоса нормализованная или горячекатаная | 6-25 | 600 | 16 | 40 | |
| ГОСТ 16523-89 | Лист горячекатаный (образцы поперечные) | До 2 2-3,9 | 550-690 | (14) (15) | — |
| Лист холоднокатаный | До 2 2-3,9 | 550-690 | (15) (16) | — | |
Механические свойства поковок (ГОСТ 8479-70)
| Термообработка | Сечение, мма | σ0,2, МПа | σв, МПа | δ5, % | ψ% | KCU, Дж/см2 | Твердость HB , не более |
| не менее | |||||||
| Нормализация | 100-300 | 245 | 470 | 19 | 42 | 39 | 143-179 |
| 300-500 | 17 | 35 | 34 | ||||
| 500-800 | 15 | 30 | 34 | ||||
| До 100 | 275 | 530 | 20 | 40 | 44 | 156-197 | |
| 100-300 | 17 | 38 | 34 | ||||
| Закалка, отпуск | 300-500 | 15 | 32 | 29 | |||
| Нормализация, закалка + отпуск | До 100 | 315 | 570 | 17 | 38 | 39 | 167-207 |
| 100-300 | 14 | 35 | 34 | ||||
| 300-500 | 12 | 30 | 29 | ||||
| До 100 | 345 | 590 | 18 | 45 | 59 | 174-217 | |
| 100-300 | 345 | 590 | 17 | 40 | 54 | 174-217 | |
| До 100 | 395 | 620 | 17 | 45 | 59 | 187-229 | |
Механические свойства в зависимости от температуры отпуска
| tот, °С | σ0,2, МПа | σв, МПа | δ5, % | ψ% | KCU, Дж/см2 | Твердость HB , не более |
| Закалка с 850 °С в воде. Образцы диаметром 15 мм | ||||||
| 450 | 830 | 980 | 10 | 40 | 59 | — |
| 500 | 730 | 830 | 12 | 45 | 78 | — |
| 550 | 640 | 780 | 16 | 50 | 98 | — |
| 600 | 590 | 730 | 25 | 55 | 118 | — |
| Закалка с 840 °С в воде. Диаметр заготовки 60 мм | ||||||
| 400 | 520-590 | 730-840 | 12-14 | 46-50 | 50-70 | 202-234 |
| 500 | 470-520 | 680-770 | 14-16 | 52-58 | 60-90 | 185-210 |
| 600 | 410-440 | 610-680 | 18-20 | 61-64 | 90-120 | 168-190 |
Механические свойства при повышенных температурах
| tисп, °С | σ0,2, МПа | σв, МПа | δ5, % | ψ% | KCU, Дж/см2 |
| Нормализация | |||||
| 200 | 340 | 690 | 10 | 36 | 64 |
| 300 | 255 | 710 | 22 | 44 | 66 |
| 400 | 225 | 560 | 21 | 65 | 55 |
| 500 | 175 | 370 | 23 | 67 | 39 |
| 600 | 78 | 215 | 33 | 90 | 59 |
| Образец диаметром 6 мм и длиной 30 мм, кованый и нормализованный. Скорость деформирования 16 мм/мин; скорость деформации 0,009 1/с | |||||
| 700 | 140 | 170 | 43 | 96 | — |
| 800 | 64 | 110 | 58 | 98 | — |
| 900 | 54 | 76 | 62 | 100 | — |
| 1000 | 34 | 50 | 72 | 100 | — |
| 1100 | 22 | 34 | 81 | 100 | — |
| 1200 | 15 | 27 | 90 | 100 | — |
Механические свойства в зависимости от сечения
| Сечение, мм | σ0,2, МПа | σв, МПа | δ5, % | ψ% | KCU, Дж/см2 |
| не менее | |||||
| 15 | 640 | 780 | 16 | 50 | 98 |
| 30 | 540 | 730 | 15 | 45 | 78 |
| 75 | 440 | 690 | 14 | 40 | 59 |
| 100 | 440 | 690 | 13 | 40 | 49 |
ПРИМЕЧАНИЕ. Закалка с 850 °С, отпуск при 550 «С. Образцы вырезали из центра заготовок.
Предел выносливости
| Характеристики прочности | σ-1, МПа | τ-1, МПа |
| σ0,2 = 310 МПа, σв = 590 МПа | 245 | 157 |
| σ0,2 = 680 МПа, σв = 880 МПа | 421 | — |
| σ0,2 = 270 МПа, σв = 520 МПа | 231 | — |
| σ0,2 = 480 МПа, σв = 660 МПа | 331 | — |
Ударная вязкость KCU
| Термообработка | KCU, Дж/см2, при температуре, °С | |||
| +20 | -20 | -40 | -60 | |
| Пруток диаметром 25 мм | ||||
| Горячая прокатка | 14-15 | 10-14 | 5-14 | 3-8 |
| Отжиг | 42-47 | 27-34 | 27-31 | 13 |
| Нормализация | 49-52 | 37-42 | 33-37 | 29 |
| Закалка + отпуск | 110-123 | 72-88 | 36-95 | 31-63 |
| Пруток диаметром 120 мм | ||||
| Горячая прокатка | 42-47 | 24-26 | 15-33 | 12 |
| Отжиг | 47-52 | 32 | 17-33 | 9 |
| Нормализация | 76-80 | 45-55 | 49-56 | 47 |
| Закалка + отпуск | 112-164 | 81 | 80 | 70 |
Технологические свойства
Температура ковки, °С: начала 1250, конца 750. Сечение до 400 мм охлаждаются на воздухе.
Обрабатываемость резанием — Кv тв.спл = 1 и Kv б.ст = 1 в горячекатаном состоянии при НВ 170-179 и σв = 640 МПа.
Склонность к отпускной хрупкости — не склонна.
Свариваемость
Сталь 45 относится к трудносвариваемым. Способы сварки: РДС и КТС. Необходим подогрев и последующая термообработка.
Прокаливаемость, мм (ГОСТ 1050-88)
Полоса прокаливаемости стали 45 после нормализации при 850 °С и закалки с 830 °С приведена на рисинке ниже.
Критический диаметр d
Физико-механические свойства стали 45 (Атомная энергетика ПНАЭ Г-7-002-86)
| Сортамент | Характеристика | Температура, К (°С) | ||||||||||||
| 293 (20) | 323 (50) | 373 (100) | 423 (150) | 473 (200) | 523 (250) | 573 (300) | 623 (350) | |||||||
| Горячекатаная сортовая сталь толщиной или диаметром до 250 мм | RTm, МПа (кгс/см2) | 598 (61) | 598 (61) | 598 (61) | 598 (61) | 598 (61) | 579 (59) | 559 (57) | 540 (55) | |||||
| RTp0,2, МПа (кгс/см2) | 353 (36) | 343 (35) | 343 (35) | 343 (35) | 343 (35) | 294 (30) | 255 (26) | 235 (24) | ||||||
| A,% | 16 | 13 | 10 | 9 | 7 | 10 | 15 | 15 | ||||||
| Z,% | 40 | 37 | 33 | 30 | 30 | 30 | 30 | 30 | ||||||
| Заготовки крепежных деталей толщиной или диаметром 300 мм, КП315* | RTm, МПа (кгс/см2) | 569 (58) | 569 (58) | 569 (58) | 569 (58) | 569 (58) | 549 (56) | 530 (54) | 510 (52) | |||||
| RTp0,2, МПа (кгс/см2) | 315 (32) | 304 (31) | 304 (31) | 294 (30) | 274 (28) | 255 (26) | 245 (25) | 225 (23) | ||||||
| A,% | 14 | 12 | 12 | 12 | 12 | 12 | 12 | 17 | ||||||
| Z,% | 35 | 33 | 33 | 33 | 33 | 33 | 35 | 35 | ||||||
| То же, от 100 до 800 мм, КП245* | RTm, МПа (кгс/мм2) | 470(48) | 470 (48) | 470 (48) | 470 (48) | 470 (48) | 461 (47) | 441 (45) | 412 (42) | |||||
| RTp0,2, МПа (кгс/мм2) | 245 (25) | 235 (24) | 235 (24) | 235 (24) | 235 (24) | 206 (21) | 177 (18) | 167 (17) | ||||||
| A, % | 14 | 12 | 10 | 8 | 6 | 8 | 13 | 13 | ||||||
| Z, % | 30 | 27 | 23 | 23 | 23 | 23 | 23 | 23 | ||||||
| То же, до 800 мм, КП275* | RTm, МПа (кгс/мм2) | 530(54) | 530(54) | 530(54) | 530(54) | 530(54) | 510(52) | 491(50) | 481(49) | |||||
| RTp0,2, МПа (кгс/мм2) | 275(28) | 265(27) | 265(27) | 265(27) | 265(27) | 226(23) | 196(20) | 196(20) | ||||||
| A, % | 12 | 10 | 8 | 6 | 5 | 8 | 11 | 11 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| То же, до 800 мм, КП315* | RTm, МПа (кгс/мм2) | 570 (58) | 570 (58) | 570 (58) | 570 (58) | 570 (58) | 549 (56) | 530 (54) | 510 (52) | |||||
| RTp0,2, МПа (кгс/мм2) | 315 (32) | 304 (31) | 304 (31) | 304 (31) | 304 (31) | 255 (26) | 226 (23) | 206 (21) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| Поковки диаметром до 300 мм, КП345* | RTm, МПа (кгс/мм2) | 590(60) | 590(60) | 590(60) | 590(60) | 590(60) | 569(58) | 549(56) | 530(54) | |||||
| RTp0,2, МПа (кгс/мм2) | 345(35) | 333(34) | 333(34) | 333(34) | 333(34) | 284(29) | 245(25) | 226(23) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
| То же, до 100 мм, КП395* | RTm, МПа (кгс/мм2) | 615(63) | 615(63) | 615(63) | 615(63) | 615(63) | 598(61) | 579(59) | 559(57) | |||||
| RTp0,2, МПа (кгс/мм2) | 395(40) | 395(40) | 395(40) | 395(40) | 395(40) | 333(34) | 294(30) | 275(28) | ||||||
| A, % | 10 | 8 | 6 | 5 | 4 | 7 | 10 | 10 | ||||||
| Z, % | 30 | 27 | 23 | 22 | 22 | 22 | 22 | 22 | ||||||
- В предел «от» и «до» включаются обе значащие цифры
- RTm — минимальное значение временного сопротивления при расчетной температуре, МПа (кгс/мм2)
- RTp0,2 — минимальное значение предела текучести при расчетной температуре, МПа (кгс/мм2)
Физические свойства
Плотность ρ кг/см3
| Марка Стали | При температуре испытаний, °С | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | 7826 | 7799 | 7769 | 7735 | 7698 | 7662 | 7625 | 7587 | 7595 | — |
Модуль нормальной упругости Е, ГПа
| Марка Стали | При температуре испытаний, °С | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | 200 | 201 | 193 | 190 | 172 | — | — | — | — | — |
Модуль упругости при сдвиге на кручение G, ГПа
Коэффициент линейного расширения α*106, К-1
| Марка стали | α*106, К-1 при температуре испытаний, °С | |||||||||
| 20-100 | 20-200 | 20-300 | 20-400 | 20-500 | 20-600 | 20-700 | 20-800 | 20-900 | 20-1000 | |
| 45 | 11,9 | 12,7 | 13,4 | 14,1 | 14,6 | 14,9 | 15,2 | — | — | — |
Коэффициент теплопроводности λ Вт/(м*К)
| Марка Стали | λ Вт/(м*К), при температуре испытаний, °С | |||||||||
| 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 45 | — | 48 | 47 | 44 | 41 | 39 | 36 | 31 | 27 | 26 |
Как определить модуль упругости стали
Выяснить модули упругости для различных марок стали можно несколькими путями:
- по справочным данным из таблиц;
- экспериментальными методами для небольшого образца;
- расчетными методами, зная необходимые данные.
Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.
Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.
В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.
| Сталь | Модуль (Е), ГПа |
| углеродистая | 195-205 |
| легированная | 206-235 |
| Ст.3, Ст.5 | 210 |
| сталь 45 | 200 |
| 25Г2С, 30ХГ2С | 200 |
Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.
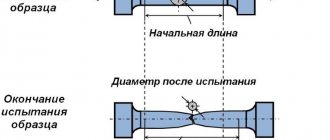
Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.
В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:
Расчеты ведут в мм и МПа.
Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела — сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
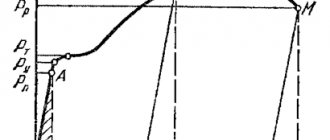
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
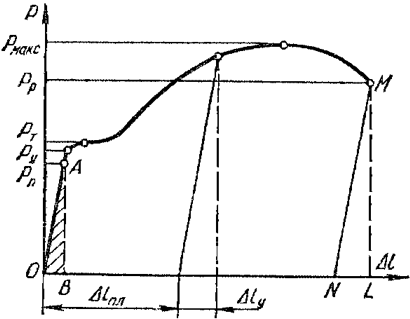

Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k — коэффициент жесткости:
k = EF/l (318.2.3)
где l — длина образца, F — площадь сечения, Е — модуль Юнга.