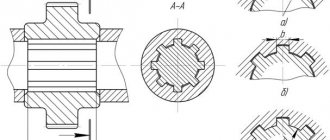
Во время работы редуктор нагревается, при этом возможно повышение давления воздуха внутри корпуса, что может привести к просачиванию масла через уплотнения и стыки. Чтобы не происходило выброса масла, внутреннюю полость редуктора делают сообщающейся с внешней средой с помощью отдушин (рис. 25, 26).
Определение основных параметров зубчатых передач редуктора
По указанию преподавателя студенты самостоятельно производят необходимые измерения и рассчитывают основные параметры редуктора.
Зубчатая передача характеризуется следующими основными параметрами:
α W – межосевое расстояние, мм; b 1 – ширина шестерни, мм;
b 2 – ширина колеса, мм; Z 1 – число зубьев шестерни; Z 2 – число зубьев колеса;
m n – модуль нормальный, мм;
β – угол наклона зубьев косозубой передачи, град.
Используя основные параметры, получают передаточное чис-
где u Т и u Б – передаточные числа тихоходной и быстроходной ступеней;
коэффициент относительной ширины колес ψ α = b 2 / α w модуль торцовый m t = 2 α w / (Z 1 +Z 2 )
модуль нормальный m n = m t cos
Обычно в косозубых передачах угол наклона зубьев β = 8. 15°,
cos β 0,99. О,97. За нормальный модуль в рассматриваемом зацеплении можно принимать модуль торцовый, округленный в меньшую сторону до ближайшего стандартного значения.
Нормальные модули зубчатых колес m n (мм) по ГОСТ 9563-
Угол наклона зубьев β = arccos ( m n / m t ).
Порядок выполнения работы
1. По методическим указаниям и плакатам изучить кинематические схемы зубчатых редукторов.
2. Выполнить пп. 1. 2, 3 протокола лабораторного журнала. Изобразить кинематическую схему редуктора, указанного преподавателем. На схеме обозначить частоты вращения валов, числа зубьев колес, вращающие моменты, межосевые расстояния.
3. Разобрать редуктор, изучить конструкцию и систему смазывания. Выполнить эскизы основных узлов и деталей по пп. 4, 5, 6, 7, 8, 9 протокола.
4. Провести необходимые измерения и выполнить расчеты по п. 10 протокола.
5. Собрать редуктор.
6. Ответить на контрольные вопросы в бланке протокола.
1. Что называют зубчатым редуктором?
2. Почему для зубчатой передачи рекомендуют применять жесткие валы?
3. Какие требования предъявляют к конструкции корпуса редуктора?
4. Каково назначение смазочного материала в редукторе?
5. Почему разъем редуктора не уплотняют упругими прокладками?
6. С какой целью шестерню делают шире колеса?
№8. Исследование конструкций волновых, планетарных редукторов и вариаторов
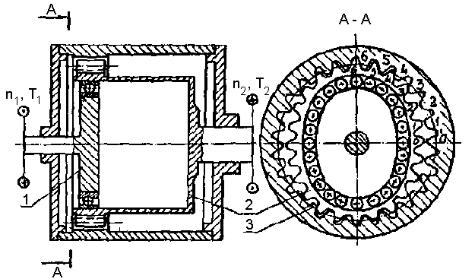
Цель работы – знакомство с конструкциями волновых и планетарных передач, сравнительная оценка их нагрузочной способности; экспериментальное определение диапазона регулирования цепного, торового и многодискового вариаторов.
1. Принцип работы и кинематика передачи волновой зубчатой передачи (ВЗП)
Передача (рис. 1) состоит из генератора волн 1, гибкого колеса 2 с внешними зубьями z 1 и жесткого колеса 3 c внутренними зубьями z 2 . Конструктивное исполнение гибких колес и генератора волн может быть различным [1]
Круглое гибкое колесо надевают на генератор волн, придающий ему овальную форму, и вводят в зацепление с жестким зубчатым
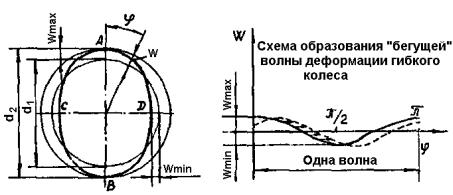
колесом. На рис. 2 показаны делительные окружности гибкого, колеса d 1 (до деформации) и жесткого колеса d 2 и упругая линия гибкого колеса W ( ϕ ) после деформации. По большой оси овала АВ (деформация W max ) зубья гибкого колеса полностью погружаются во впадины жесткого, по малой (деформация W min ) вершины зубьев колес стоят один против другого, не зацепляясь. Общее число контактирующих пар зубьев доходит до 40% от числа зубьев гибкого колеса
При вращении генератора по гибкому колесу бежит волна деформации с частотой вращения генератора (рис. 2). За четверть оборота генератора для двухволновой передачи зуб гибкого колеса, находившийся в вершине волны и полностью погруженный во впадину жесткого колеса (рис. 1, положение 6), окажется в минимуме волны деформация и выйдет из зацепления с жестким колесом, заняв положение 0 – «зуб против зуба».
За четверть оборота генератора гибкое колесо повернулось относительно жесткого только на половину окружного делительного шага Р /2. При полном обороте генератора этот поворот будет равен 2 Р, что соответствует разности чисел зубьев жесткого и гибкого колес (Z 2 -Z 1 ) . P . Полный оборот гибкого колеса произойдет через Z 1 /(Z 2 -Z 1 ) оборотов генератора волн; направления вращения гибкого колеса и генератора противоположны.
Следовательно, передаточное отношение одноступенчатого волнового зубчатого редуктора при остановленном неподвижном же-
U = − Z 1 ( Z 2 − Z 1 )
Читать также: Толстая фольга для чеканки
*) Двухволновой называется передача, у которой гибкое колесо деформировано овальным генератором волн так, что за один оборот генератора в гибком колесе дважды возникает деформация.

Умножим числитель и знаменатель правой части предыдущего выражения на модуль m . Тогда
Таким образом, передаточное отношение волновой зубчатой передачи определяется отношением делительного диаметра гибкого колеса к его удвоенной радиальной деформации. Знак «минус» показывает, что вращение ведущего и ведомого элементов происходит в разные стороны.
С увеличением радиальной деформации при одном и том же диаметре гибкого колеса d 1 – растут напряжения изгиба в колесе, и понижается его усталостная прочность. Поэтому нижний предел передаточных отношений ВЗП составляет 60….80, что соответствует W max =1/100 d 1 . Верхний предел передаточных отношений при заданном диаметре гибкого колеса ограничен
возможностью нарезания зубьев мелкого модуля m≥ 0,15 мм и обычно составляет не более 300 в одной ступени (паре зубчатых колес).
Основные достоинства ВЗП – высокая нагрузочная способность и кинематическая точность за счет большого числа пар зубьев в одновременном зацеплении и большое передаточное отношение в одной ступени.
Допускаемый вращающий момент ВЗП зависит от передаточного отношения:
при U U ≥100 – долговечностью подшипников генератора волн. Расчет ВЗП можно найти в [2] .
Многопарность зацепления определяет высокую перегрузочную способность ВЗП. Кратковременно можно допускать трех-, пятикратные перегрузки. При увеличении вращающего момента сверх номинального происходит искажение формы гибкого колеса и падение КПД передачи, так как растут потери в генераторе волн. Искажение формы гибкого колеса тем меньше, чем больше площадь его опирания на генератор волн
Конструкция гибких колес и генераторов волн
Основные типы и соотношения размеров гибких колес и генераторов волн даны в атласе [1].
Для передач, в которых люфт не допустим, применяют гибкие колеса с дном или фланцем. Чтобы уменьшить напряжения в гибком колесе при деформации, толщину диафрагмы, соединяющей оболочку с жестким дном или фланцем, берут такой же, как толщина гладкой части оболочки; длина оболочки в этом случае L = (0,5. . 0,8) d 1 . При необходимости сокращения осевых габаритов применяют шлицевое соединение гибкого колеса с тихоходным валом. В этом случае L = (0,3. 0,8) d 1 . Шлицы, как правило, выполняют тем же инструментом, что и основной зубчатый венец – это упрощает технологию изготовления. В предельном случае гибкое колесо может быть выполнено в виде кольца с шириной, равной ширине зубчатого венца, и торцевыми шлицами.
Гибкие колеса изготавливают из холоднотянутых труб или поковок. После термообработки заготовки (улучшение, твердость
HRC) растачивают внутренний диаметр под генератор волн. По этому диаметру заготовку гибкого колеса надевают на массивную оправку, обеспечивающую жесткость тонкостенной конструкции при обработке наружной поверхности и нарезании зубьев.
Кулачковый генератор волн. Состоит из овального кулачка, выполненного по рассчитанной форме деформации гибкого колеса W ( ϕ ) и специального гибкого подшипника [2] с тонкими кольцами, чтобы обеспечить возможность его деформирования.
Наружное кольцо подшипника деформируется периодически и работает на знакопеременный изгиб; внутреннее – деформируется однократно при запрессовке подшипника на кулачок.
ВЗП с таким генератором имеет наименьшее число деталей, обладает наибольшей нагрузочной способностью, так как размеры подшипника максимально возможные и гибкое колесо оперто на генератор по всему периметру.
Дисковый генератор волн . Состоит из эксцентрикового вала и двух дисков. Каждый диск расположен на двух подшипниках. Размеры дисков и эксцентриситета е обеспечивают расчетную форму деформации гибкого колеса W ( ϕ ), опирающегося на генератор по дуге в 60…80 0 в каждой волне деформации. В силовых передачах между гибким колесом и роликами ставят твердое (HRC>40) подкладное кольцо, чтобы избежать «раскатки».
Дисковый генератор содержит много деталей, но их можно изготовить на токарном станке. Он малоинерционен, так как диски вращаются с малой частотой. Обладает сравнительно высокой нагрузочной способностью.
Четырехроликовый генератор волн . Состоит из водила и за-
крепленных в нем на осях четырех роликов. Каждый ролик сидит на двух подшипниках.
Установка пары роликов под углом 2 β =60 ° обеспечивает расчетную двухволновую форму деформации гибкого колеса W ( ϕ ). Четырехроликовый генератор наиболее прост в изготовлении, но передача с таким генератором обладает малой нагрузочной способностью, так как гибкое колесо опирается на генератор только в четырех точках.
Читать также: Как шуруповерт подключить на 220 вольт
Размеры подшипников в роликах ограничены, а частота вращения выше частоты вращения быстроходного вала.
2. Планетарные передачи
Планетарным называется механизм, состоящий из зубчатых колес, в котором геометрическая ось хотя бы одного из колес подвижна.
Планетарные передачи по сравнению с обычными имеют преимущества: меньшие габариты и массу, так как вращающий момент передается по нескольким потокам (сателлитам). В некоторых
схемах можно получить большие передаточные отношения
лом количестве колес. Нужно помнить, что с увеличением
точного числа в одной передаче КПД падает.
К недостаткам передач можно отнести: требование повышен-
ной точности изготовления, большое количество подшипников качения, необходим долбяк для нарезания колес с внутренними зубьями (долбяк меняет параметры при переточках).
Простая планетарная передача (рис.3) включает: ″a ″ (z а) , ″b″ (z b ) – центральные колеса с внешними и внутренними зубьями, ″g″ (z g ) – сателлиты с внешними зубьями, которые зацепляются одновременно с ″a″ и ″b″ (z -числа зубьев колес, n w -число сателлитов, здесь n w = 3), ″h″- водило, на котором расположены оси сателлитов (здесь водило соединено с тихоходным валом).
Принцип работы: при закрепленном колесе ″b″ ( ω b = 0) вращение колеса ″a″ ( ω а ) вызывает вращение сателлита ″g″ относительно собственной оси со скоростью ω g . Качение сателлита по ″b″ перемещает его ось и вращает водило со скоростью ω h .
Сателлит совершает вращение относительно водила со скоростью ω h g = ω g – ω h и вместе с водилом (переносное движение). Его движения напоминают движения планет, поэтому передача называется планетарной.
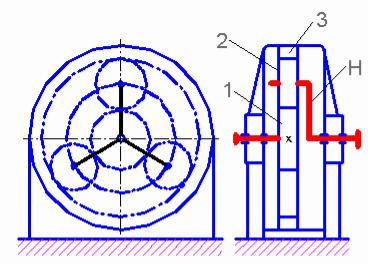

Основными звеньями планетарной передачи называют такие, которые воспринимают внешние моменты. На рис. 3 основные звенья
– ″a″, ″b″, ″h″, т.е. два центральных колеса (2К) и водило (h). Сокращенно обозначают 2К-h. Внешние моменты T а – на ведущем вале, T h –
на ведомом (тихоходном) вале, T b – на колесе z b (на корпусе).
Любое основное звено планетарной передачи может быть
Дифференциальной называют передачу, в которой все основ-
ные звенья подвижны. При этом можно суммировать движение
звеньев на одном или раскладывать движение одного звена на 2 остальных.
Наиболее распространенные схемы передач .
Наиболее распространенные схемы приведены ниже. Они обладают или высоким КПД или большими переда точными отношениями в одной передаче.
Схема 1 (рис. 3 ) – одноступенчатая передача (2К-h – два цен-
тральных колеса и водило), наиболее распространена, так как
высокий КПД и технологичную конструкцию. Наибольшее
Зубча́тое колесо́
или
шестерня́
[1] ,
зубчатка
[2] — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.
Обычно термины зубчатое колесо
,
шестерня
,
зубчатка
являются синонимами, но некоторые авторы называют ведущее зубчатое колесо
шестернёй
, а ведомое — колесом [2] . Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось») [3] .
Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим
, а колесо, с которого момент снимается —
ведомым
. Если диаметр ведущего колеса
меньше
, то крутящий момент ведомого колеса
увеличивается
за счёт пропорционального
уменьшения
скорости вращения,
и наоборот
. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.


Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
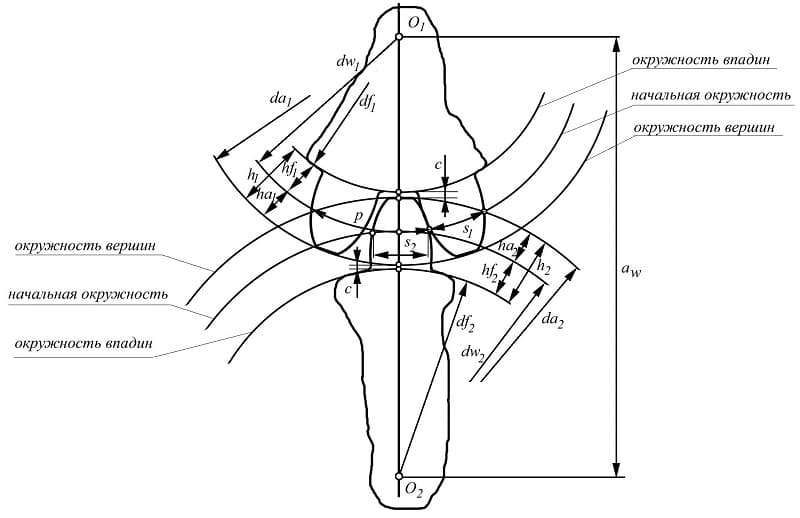

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Характеристики и применение
Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.
В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.
Используется в подвижных частях механизмов соместно с зубчатой рейкой.
Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.
Параметры модуля шестерни
Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:
- диаметр делительной окружности;
- шаг и число зубьев;
- эвольвент (диаметр основной окружности);
- аналогичная характеристика впадин темной шестеренки;
- высота зуба темного и светлого колеса.
В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.
Что такое модуль на чертеже?
Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Различают высотную коррекцию ( xΣ(d)
=
) и угловую (
xΣ(d)≠
).
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых.
Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь
на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Прошу
уважающих труд автораскачивать файлпосле подпискина анонсы статей!
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как обозначается делительный диаметр?
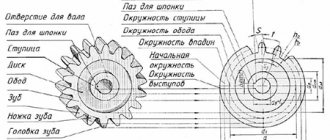
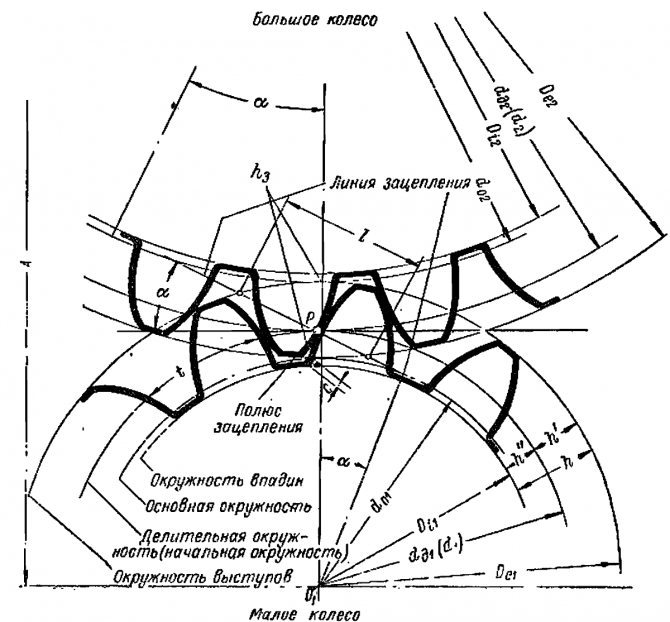
Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.
Основные определения из теории зацепления шестерен
Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой
Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение: d д = mZ Если шестерни не имеют коррекции, то начальные и делительные окружности совпадают
Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев
Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев d = d дcosα
Шагом t называется расстояние по дуге делительной окружности между одноименными профилями соседних зубьев
Основным шагом t называется шаг по основной окружности
Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к π
Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности
Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ — прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям
Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров
Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса
Коэффициентом перекрытия ε называется отношение дуги зацепления к основному шагу
Коэффициентом коррекции ξ называется отношение величины профильного смещения к модулю
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
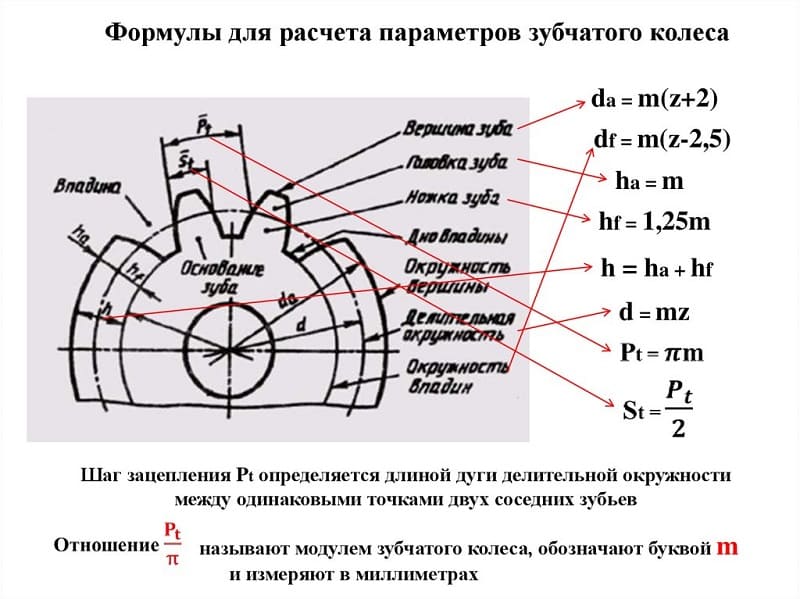

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
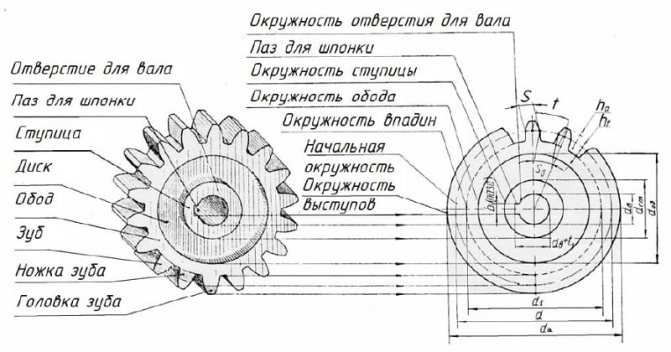

Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Обозначения для расчёта шестерней по формулам.

К вашему вниманию все обозначения какие вам понадобятся для расчета по формулам параметров шестерней. В данной таблице представлены основные обозначения параметров цилиндрических зубчатых колес:
- Высота зуба (полная).
- Высота головки зуба от окружности выступов до делительной окружности.
- Высота ножки зуба от делитель-ной окружности до окружности впадин.
- Глубина замера толщины зуба.
- Глубина захода зубьев, равная сумме высот головок зубьев (рабочая высота зуба).
- Диаметр начальной окружности.
- Диаметр делительной окружности.
- Диаметр основной окружности.
- Диаметр окружности выступов.
- Диаметр окружности впадин.
- Длина зацепления.
- Зазор радиальный в зубчатой паре.
- Зазор боковой в зубчатой паре.
- Зазор боковой в торцовом сечении.
- Зазор боковой в нормальном сечении.
- Коэффициент сдвига осей.
- Коэффициент высоты зуба инструмента (исходного контура).
- Коэффициент высоты зуба инструмента по отношению к модулю в нормальном, сечении.
- Коэффициент высоты зуба инструмента по отношению к модулю в торцовом сечении.
- Коэффициент сдвига исходного контура (инструмента).
- Коэффициент сдвига исходного контура (инструмента) минимальный при котором нет подрезания.
- Коэффициент сдвига исходного контура максимальный.
- Коэффициент сдвига исходного контура (инструмента) при заостренных зубьях.
- Коэффициент перекрытия.
- Коэффициент перекрытия в торцовой плоскости для косозубых колес.
- Модуль торцовый.
- Модуль нормальный.
- Межцентровое (межосевое) расстояние сцепляющейся пары колес.
- Межцентровое расстояние фаузацепления .
- Питч диаметральный.
- Питч окружной.
- Половина угловой толщины зуба на делительной окружности.
- Разность сдвигов—разность коэффициентов коррекции при внутреннем зацеплении.
- Сумма сдвигов исходного контура.
- Сумма коэффициентов коррекции сцепляющихся колес.
- Сумма чисел зубьев сцепляющихся колес при внутреннем зацеплении.
- Сумма чисел зубьев сцепляющихся колес при наружном зацеплении.
- Толщина зуба номинальная по хорде делительной окружности.
- Толщина зуба по дуге делительной окружности номинальная (без обязательного утонения) — для прямозубых колес.
- Толщина зуба номинальная по постоянной хорде для прямозубых колес.
- Толщина зуба номинальная по постоянной хорде для косозубых колес в нормальном сечении.
- Толщина зуба номинальная по постоянной хорде для косозубых колес в торцовом сечении.
- Толщина зуба по дуге окружности выступов.
- Толщина, зуба по постоянной хорде верхний предельный размер.
- Толщина зубьев по общей нормали для прямозубых колес .
- Толщина зубьев по общей нормали для прямозубых колес (или реек) — верхний предельный размер.
- Толщина зубьев по общей нормали для косозубых колес в нормальном сечении.
- Толщина зубьев по общей нормали для косозубых колес в нормальном сечении — верхний предельный размер.
- Угол зацепления пары колес.
- Угол зацепления косозубых колес в торцовом сечении.
- Угол инструмента профильный (исходного контура).
- Угол инструмента в нормальном сечении профильный.
- Угол инструмента в,торцовом сечении профильный.
- Угол наклона зубьев на основном цилиндре.
- Угол наклона зубьев на делительном цилиндре.
- Число зубьев.
- Число зубьев колеса, свободного от подрезания, минимальное.
- Число зубьев колеса практически допускаемое минимальное.
- Число зубьев, охватываемых размером.
- Шаг по делительной окружности.
- Шаг основной.
- Шаг торцовый.
- Шаг нормальный.
- Ширина зубчатого венца.

Заказ: Шестерня, диск. Модуль шесть.
Предыдущая запись

Исходный контур зубчатых колёс.
Следующая запись
Какие бывают зубчатые колеса?
Виды зубчатых колес, шестерен
- Поперечный профиль зуба Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. …
- Продольная линия зуба Прямозубые шестерни …
- Шестерни с внутренним зацеплением …
- Винтовые шестерни …
- Секторные шестерни …
- Шестерни с круговыми зубьями
Прямозубые и косозубые колесики
Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.
Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.


Шевронные модификации и аналоги с внутренним зацеплением
Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).
Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.
Винтовые, круговые, секторные версии
Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.
Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.
Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.


Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
В чем заключаются сходства между шестерней и зубчатым колесом
Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:
- Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
- У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
- При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
- Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
- Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.
Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.
Стандарты зубчатых передач США
Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
Р = z/d = z/(z • m/25,4) =25,4/m
Для перевода стандарта США в европейский стандарт служит зависимость:
m = 25,4 мм / P
Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
CP = (25,4 мм / P) π.
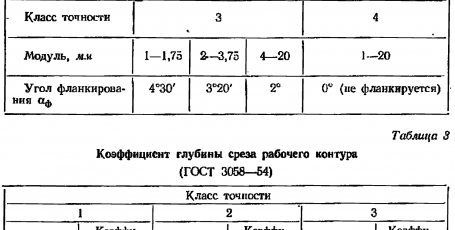
Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
Обозначение (пример): Р 5 /7
Р = 7 для расчета головки зуба,
Р = 5 для расчета других параметров.
Система обозначений и преобразований
Диаметр окружности выступов: OD = da.
Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
Диаметр окружности впадин: RD = df
LD =(N+2x) / P (в дюймах)
LD= (N+2x)·m (в мм).
где dw — диаметральный модуль.
Подытожим
Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.
Источники
- https://mehmanxona.ru/tehnologii/vidy-shesterenok.html
- https://novoe-info.ru/chto-takoe-modul-shesterni/
- https://MechPrivod.com/market/zubchataya_shesterenka/shesterenka_zubchataya_cilindricheskaya/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://FB.ru/article/429020/modul-shesterni-vidyi-opredelenie-standartnyie-pokazateli
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .
Цилиндрические шестерни
Поперечный профиль зуба
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например – передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
Модуль шестерни (m
) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:
d
— диаметр делительной окружности
z
— число зубьев шестерни
d
a — диаметр окружности вершин темной шестерни
d
b — диаметр основной окружности – эвольвенты
d
f — диаметр окружности впадин темной шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба – h
aP и высота ножки зуба –
h
fP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем
m
следующим образом:
h
aP =
m
;
h
fP =
1,2 m
, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни – самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами – плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Читать также: Типы разъемов для монитора
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.